

End Behavior
In this section you’ll learn what end behavior is, how to identify end behavior by looking at the leading coefficient and the sign of the leading coefficient, and how that ties into the number of x – intercepts.
Read through the notes below, watch the video, try the practice problems. Learning new material is always difficult and confusing. In fact, it requires you to develop and then relief confusion, and often frustration. But, the end result is worth it because learning is an activity worth it’s own efforts.
When we discuss “end behavior” of a polynomial function we are talking about what happens to the outputs ( y values) when x is really small, or really large. Another way to say this is, what do the far left and far right of the graph look like?
For the graph to the left, we can describe the end behavior on the left as “going up.” We can describe the behavior on the right as “going up,” as well.
In truth, on the left, as you learned in the last section, the graph is decreasing. On the right it is increasing.
In this section you will learn to separate all possible polynomial functions into two basic categories, even and odd. You will learn the possible end behavior possibilities of each based on the sign of the leading coefficient and whether the degree is even or odd. Let’s get to it!
To determine if a polynomial function is even or odd you examine the degree. If the degree is even, we call the polynomial function even. If the degree is odd, we call the polynomial function odd. That’s it!
So, f ( x ) = 5 x 7 is an odd function because the degree is 7.
The reason we separate even and odd functions is because of the sign of a negative base raised to an exponent. If the exponent is even, the product is always positive. If the exponent is odd, the product is negative. To be explicitly clear, look at the exploration below.
This happens because a negative number times another negative number is positive. So every pair of odd numbers has an even product.
(-2)(-2) = 4
But, when you have an odd number of that base, the pairs will all be positive, with one extra negative number left over, making the final product negative.
(-2)(-2)(-2) = -8
Let’s do a simple chart comparing two functions, one a degree of 5, the other a degree of 4. We will only plug in negative numbers.
In the table above we only showed negative inputs. That is because a positive base to the power of any integer is positive. Let’s look at the graph of each now. The first table will compare a rather global view of each graph. But the second will zoom in on the “left” side of the coordinate plane, where the x – values are negative. This will allow us to see how the table above translates to the graph.
Remember, a graph is a picture of all solutions to an equation (in our context). Look at how the graph of each function behaves in quadrants 2 and 3. In quadrants 2 and 3, x is always negative, and x is the input.
For small values of x (small meaning negative numbers and on the “left” of the coordinate plane), the odd function is increasing while the even function is decreasing. For both functions, the odd and even, the “right” side of the coordinate plane showed both graphs to be increasing.
Let’s look at each graph again and discuss some common language here.
There is one remaining piece of the puzzle we need to understand. After that, we’ll look at a chart that will help make all of this clear and easily referenced.
In both of our examples, the leading coefficient was positive. If you recall with quadratic equations, when a is negative, the parabola goes down. One way to think of this is that it is flipped over. The same holds true for other polynomial functions. Let’s see a t-chart to show how this works algebraically. Then, we’ll look at the graphs.
The key here is not to confuse our verbal descriptions with increasing and decreasing. For the graph of y = – x 5 we say, “up on the left and down on the right.” However, it is decreasing on both sides. Do you see that odd functions can be described as heading in opposite directions on each side? Even functions either go up both ways, or down both ways. Let’s take a look at that.
Let’s pull it all together now, shall we. In the chart below you can see how the end behavior of even and odd functions looks, for both positive leading coefficients and negative leading coefficients. Remember, odd functions go opposite directions and even functions go the same direction.
End behavior describes what the output ( y ) or f ( x ) does as x grows infinitely small (to the left, x → -∞), or as x grows infinitely large (to the right, x → ∞). As x grows infinitely small, if the outputs are increasing, we say this is “up left.”
As x grows infinitely small, if the outputs are decreasing, we say this is “down left.”
As x grows infinitely large, if the outputs are increasing, we say this is “up right.”
As x grows infinitely large, if the outputs are decreasing, we say this is “down right.”
- Even functions with a positive leading coefficient “go up both ways.”
- Even functions with a negative leading coefficient “go down both ways.”
- Odd functions with a positive leading coefficient “go down left, up right.”
- Odd functions with a negative leading coefficient “go up left, down right.”
To see a review of the assignment and to summarize what we’ve learned to date about polynomial functions, watch the video below.
Consider making your next Amazon purchase using our Affiliate Link. You get the same prices, service and shipping at no extra cost, but a small portion of your purchase price will go to help maintaining this site!
Can't Find Something?
Email address:
Quality resources and hosting are expensive
Help Keep Access Free

Social Media Links
- YouTube Channel
- FaceBook Page
Get Started

Become a math whiz with AI Tutoring, Practice Questions & more.
End Behavior of a Function
The end behavior of a polynomial function is the behavior of the graph of f ( x ) as x approaches positive infinity or negative infinity.
The degree and the leading coefficient of a polynomial function determine the end behavior of the graph.
The leading coefficient is significant compared to the other coefficients in the function for the very large or very small numbers. So, the sign of the leading coefficient is sufficient to predict the end behavior of the function.
| |||
| Even | Positive | Example:
| |
| Even | Negative | Example:
| |
| Odd | Positive | Example:
| |
| Odd | Negative | Example:
|
To predict the end-behavior of a polynomial function, first check whether the function is odd-degree or even-degree function and whether the leading coefficient is positive or negative.
Find the end behavior of the function x 4 − 4 x 3 + 3 x + 25 .
The degree of the function is even and the leading coefficient is positive. So, the end behavior is:
f ( x ) → + ∞ , as x → − ∞ f ( x ) → + ∞ , as x → + ∞
The graph looks as follows:
- NNAT Test Prep
- CLEP English Literature Test Prep
- Actuarial Exam FM Test Prep
- GRE Subject Test in Physics Test Prep
- Exam P - Probability Test Prep
- IB Classical Languages HL Tutors
- GRE Subject Test in Biology Test Prep
- Glaciology Tutors
- 5th Grade Tutors
- AANP - American Association of Nurse Practitioners Test Prep
- Nationalism Studies Tutors
- HSPT Tutors
- Videography Tutors
- CLEP Principles of Microeconomics Test Prep
- AFSP - Annual Filing Season Program Courses & Classes
- Pharmaceutical Sciences Tutors
- African History Tutors
- CLS - Clinical Laboratory Science Courses & Classes
- ARM-P - Associate in Risk Management for Public Entities Courses & Classes
- Michigan Bar Exam Courses & Classes
- Buffalo Tutoring
- Cleveland Tutoring
- Phoenix Tutoring
- Atlanta Tutoring
- Raleigh-Durham Tutoring
- Philadelphia Tutoring
- Syracuse Tutoring
- Orlando Tutoring
- Spokane Tutoring
- Nashville Tutoring
- Math Tutors in Houston
- Computer Science Tutors in Philadelphia
- Reading Tutors in Seattle
- GMAT Tutors in Chicago
- Biology Tutors in Seattle
- GMAT Tutors in New York City
- SAT Tutors in Houston
- Math Tutors in Seattle
- Statistics Tutors in Philadelphia
- Spanish Tutors in Boston
5.2 Power Functions and Polynomial Functions
Learning objectives.
In this section, you will:
- Identify power functions.
- Identify end behavior of power functions.
- Identify polynomial functions.
- Identify the degree and leading coefficient of polynomial functions.
Suppose a certain species of bird thrives on a small island. Its population over the last few years is shown in Table 1 .
The population can be estimated using the function P ( t ) = − 0.3 t 3 + 97 t + 800 , P ( t ) = − 0.3 t 3 + 97 t + 800 , where P ( t ) P ( t ) represents the bird population on the island t t years after 2009. We can use this model to estimate the maximum bird population and when it will occur. We can also use this model to predict when the bird population will disappear from the island. In this section, we will examine functions that we can use to estimate and predict these types of changes.
Identifying Power Functions
Before we can understand the bird problem, it will be helpful to understand a different type of function. A power function is a function with a single term that is the product of a real number, a coefficient, and a variable raised to a fixed real number.
As an example, consider functions for area or volume. The function for the area of a circle with radius r r is
and the function for the volume of a sphere with radius r r is
Both of these are examples of power functions because they consist of a coefficient, π π or 4 3 π , 4 3 π , multiplied by a variable r r raised to a power.
Power Function
A power function is a function that can be represented in the form
where k k and p p are real numbers, and k k is known as the coefficient .
Is f ( x ) = 2 x f ( x ) = 2 x a power function?
No. A power function contains a variable base raised to a fixed power. This function has a constant base raised to a variable power. This is called an exponential function, not a power function.
Which of the following functions are power functions?
f ( x ) = 1 Constant function f ( x ) = x Identity function f ( x ) = x 2 Quadratic function f ( x ) = x 3 Cubic function f ( x ) = 1 x Reciprocal function f ( x ) = 1 x 2 Reciprocal squared function f ( x ) = x Square root function f ( x ) = x 3 Cube root function f ( x ) = 1 Constant function f ( x ) = x Identity function f ( x ) = x 2 Quadratic function f ( x ) = x 3 Cubic function f ( x ) = 1 x Reciprocal function f ( x ) = 1 x 2 Reciprocal squared function f ( x ) = x Square root function f ( x ) = x 3 Cube root function
All of the listed functions are power functions.
The constant and identity functions are power functions because they can be written as f ( x ) = x 0 f ( x ) = x 0 and f ( x ) = x 1 f ( x ) = x 1 respectively.
The quadratic and cubic functions are power functions with whole number powers f ( x ) = x 2 f ( x ) = x 2 and f ( x ) = x 3 . f ( x ) = x 3 .
The reciprocal and reciprocal squared functions are power functions with negative whole number powers because they can be written as f ( x ) = x − 1 f ( x ) = x − 1 and f ( x ) = x − 2 . f ( x ) = x − 2 .
The square and cube root functions are power functions with fractional powers because they can be written as f ( x ) = x 1 2 f ( x ) = x 1 2 or f ( x ) = x 1 3 . f ( x ) = x 1 3 .
Which functions are power functions?
f ( x ) = 2 x ⋅ 4 x 3 g ( x ) = − x 5 + 5 x 3 h ( x ) = 2 x 5 − 1 3 x 2 + 4 f ( x ) = 2 x ⋅ 4 x 3 g ( x ) = − x 5 + 5 x 3 h ( x ) = 2 x 5 − 1 3 x 2 + 4
Identifying End Behavior of Power Functions
Figure 2 shows the graphs of f ( x ) = x 2 , g ( x ) = x 4 f ( x ) = x 2 , g ( x ) = x 4 and h ( x ) = x 6 , h ( x ) = x 6 , which are all power functions with even, positive integer powers. Notice that these graphs have similar shapes, very much like that of the quadratic function in the toolkit. However, as the power increases, the graphs flatten somewhat near the origin and become steeper away from the origin.
To describe the behavior as numbers become larger and larger, we use the idea of infinity. We use the symbol ∞ ∞ for positive infinity and −∞ −∞ for negative infinity. When we say that “ x x approaches infinity,” which can be symbolically written as x → ∞ , x → ∞ , we are describing a behavior; we are saying that x x is increasing without bound.
With the positive even-power function, as the input increases or decreases without bound, the output values become very large, positive numbers. Equivalently, we could describe this behavior by saying that as x x approaches positive or negative infinity, the f ( x ) f ( x ) values increase without bound. In symbolic form, we could write
Figure 3 shows the graphs of f ( x ) = x 3 , g ( x ) = x 5 , f ( x ) = x 3 , g ( x ) = x 5 , and h ( x ) = x 7 , h ( x ) = x 7 , which are all power functions with odd, whole-number powers. Notice that these graphs look similar to the cubic function in the toolkit. Again, as the power increases, the graphs flatten near the origin and become steeper away from the origin.
These examples illustrate that functions of the form f ( x ) = x n f ( x ) = x n reveal symmetry of one kind or another. First, in Figure 2 we see that even functions of the form f ( x ) = x n , n f ( x ) = x n , n even, are symmetric about the y - y - axis. In Figure 3 we see that odd functions of the form f ( x ) = x n , n f ( x ) = x n , n odd, are symmetric about the origin.
For these odd power functions, as x x approaches negative infinity, f ( x ) f ( x ) decreases without bound. As x x approaches positive infinity, f ( x ) f ( x ) increases without bound. In symbolic form we write
The behavior of the graph of a function as the input values get very small ( x → − ∞ x → − ∞ ) and get very large ( x → ∞ x → ∞ ) is referred to as the end behavior of the function. We can use words or symbols to describe end behavior.
Figure 4 shows the end behavior of power functions in the form f ( x ) = k x n f ( x ) = k x n where n n is a non-negative integer depending on the power and the constant.
Given a power function f ( x ) = k x n f ( x ) = k x n where n n is a positive integer, identify the end behavior.
- Determine whether the power is even or odd.
- Determine whether the constant is positive or negative.
- Use Figure 4 to identify the end behavior.
Identifying the End Behavior of a Power Function
Describe the end behavior of the graph of f ( x ) = x 8 . f ( x ) = x 8 .
The coefficient is 1 (positive) and the exponent of the power function is 8 (an even number). As x x approaches infinity, the output (value of f ( x ) f ( x ) ) increases without bound. We write as x → ∞ , f ( x ) → ∞ . x → ∞ , f ( x ) → ∞ . As x x approaches negative infinity, the output increases without bound. In symbolic form, as x → − ∞ , f ( x ) → ∞ . x → − ∞ , f ( x ) → ∞ . We can graphically represent the function as shown in Figure 5 .
Identifying the End Behavior of a Power Function.
Describe the end behavior of the graph of f ( x ) = − x 9 . f ( x ) = − x 9 .
The exponent of the power function is 9 (an odd number). Because the coefficient is –1 –1 (negative), the graph is the reflection about the x - x - axis of the graph of f ( x ) = x 9 . f ( x ) = x 9 . Figure 6 shows that as x x approaches infinity, the output decreases without bound. As x x approaches negative infinity, the output increases without bound. In symbolic form, we would write
We can check our work by using the table feature on a graphing utility.
| –10 | 1,000,000,000 |
| –5 | 1,953,125 |
| 0 | 0 |
| 5 | –1,953,125 |
| 10 | –1,000,000,000 |
We can see from Table 2 that, when we substitute very small values for x , x , the output is very large, and when we substitute very large values for x , x , the output is very small (meaning that it is a very large negative value).
Describe in words and symbols the end behavior of f ( x ) = − 5 x 4 . f ( x ) = − 5 x 4 .
Identifying Polynomial Functions
An oil pipeline bursts in the Gulf of Mexico, causing an oil slick in a roughly circular shape. The slick is currently 24 miles in radius, but that radius is increasing by 8 miles each week. We want to write a formula for the area covered by the oil slick by combining two functions. The radius r r of the spill depends on the number of weeks w w that have passed. This relationship is linear.
We can combine this with the formula for the area A A of a circle.
Composing these functions gives a formula for the area in terms of weeks.
Multiplying gives the formula.
This formula is an example of a polynomial function . A polynomial function consists of either zero or the sum of a finite number of non-zero terms, each of which is a product of a number, called the coefficient of the term, and a variable raised to a non-negative integer power.
Polynomial Functions
Let n n be a non-negative integer. A polynomial function is a function that can be written in the form
This is called the general form of a polynomial function. Each a i a i is a coefficient and can be any real number, but a n ≠ 0 a n ≠ 0 . Each expression a i x i a i x i is a term of a polynomial function .
Which of the following are polynomial functions?
The first two functions are examples of polynomial functions because they can be written in the form f ( x ) = a n x n + ... + a 2 x 2 + a 1 x + a 0 , f ( x ) = a n x n + ... + a 2 x 2 + a 1 x + a 0 , where the powers are non-negative integers and the coefficients are real numbers.
- f ( x ) f ( x ) can be written as f ( x ) = 6 x 4 + 4. f ( x ) = 6 x 4 + 4.
- g ( x ) g ( x ) can be written as g ( x ) = − x 3 + 4 x . g ( x ) = − x 3 + 4 x .
- h ( x ) h ( x ) cannot be written in this form and is therefore not a polynomial function.
Identifying the Degree and Leading Coefficient of a Polynomial Function
Because of the form of a polynomial function, we can see an infinite variety in the number of terms and the power of the variable. Although the order of the terms in the polynomial function is not important for performing operations, we typically arrange the terms in descending order of power, or in general form. The degree of the polynomial is the highest power of the variable that occurs in the polynomial; it is the power of the first variable if the function is in general form. The leading term is the term containing the highest power of the variable, or the term with the highest degree. The leading coefficient is the coefficient of the leading term.
Terminology of Polynomial Functions
We often rearrange polynomials so that the powers are descending.
When a polynomial is written in this way, we say that it is in general form.
Given a polynomial function, identify the degree and leading coefficient.
- Find the highest power of x x to determine the degree of the function.
- Identify the term containing the highest power of x x to find the leading term.
- Identify the coefficient of the leading term.
Identify the degree, leading term, and leading coefficient of the following polynomial functions.
For the function f ( x ) , f ( x ) , the highest power of x x is 3, so the degree is 3. The leading term is the term containing that degree, −4 x 3 . −4 x 3 . The leading coefficient is the coefficient of that term, −4. −4.
For the function g ( t ) , g ( t ) , the highest power of t t is 5 , 5 , so the degree is 5. 5. The leading term is the term containing that degree, 5 t 5 . 5 t 5 . The leading coefficient is the coefficient of that term, 5. 5.
For the function h ( p ) , h ( p ) , the highest power of p p is 3 , 3 , so the degree is 3. 3. The leading term is the term containing that degree, − p 3 . − p 3 . The leading coefficient is the coefficient of that term, −1. −1.
Identify the degree, leading term, and leading coefficient of the polynomial f ( x ) = 4 x 2 − x 6 + 2 x − 6. f ( x ) = 4 x 2 − x 6 + 2 x − 6.
Identifying End Behavior of Polynomial Functions
Knowing the degree of a polynomial function is useful in helping us predict its end behavior. To determine its end behavior, look at the leading term of the polynomial function. Because the power of the leading term is the highest, that term will grow significantly faster than the other terms as x x gets very large or very small, so its behavior will dominate the graph. For any polynomial, the end behavior of the polynomial will match the end behavior of the power function consisting of the leading term. See Table 3 .
| Polynomial Function | Leading Term | Graph of Polynomial Function |
|---|---|---|
Identifying End Behavior and Degree of a Polynomial Function
Describe the end behavior and determine a possible degree of the polynomial function in Figure 7 .
As the input values x x get very large, the output values f ( x ) f ( x ) increase without bound. As the input values x x get very small, the output values f ( x ) f ( x ) decrease without bound. We can describe the end behavior symbolically by writing
In words, we could say that as x x values approach infinity, the function values approach infinity, and as x x values approach negative infinity, the function values approach negative infinity.
We can tell this graph has the shape of an odd degree power function that has not been reflected, so the degree of the polynomial creating this graph must be odd and the leading coefficient must be positive.
Describe the end behavior, and determine a possible degree of the polynomial function in Figure 8 .
Given the function f ( x ) = − 3 x 2 ( x − 1 ) ( x + 4 ) , f ( x ) = − 3 x 2 ( x − 1 ) ( x + 4 ) , express the function as a polynomial in general form, and determine the leading term, degree, and end behavior of the function.
Obtain the general form by expanding the given expression for f ( x ) . f ( x ) .
The general form is f ( x ) = −3 x 4 − 9 x 3 + 12 x 2 . f ( x ) = −3 x 4 − 9 x 3 + 12 x 2 . The leading term is −3 x 4 ; −3 x 4 ; therefore, the degree of the polynomial is 4. The degree is even (4) and the leading coefficient is negative (–3), so the end behavior is
Given the function f ( x ) = 0.2 ( x − 2 ) ( x + 1 ) ( x − 5 ) , f ( x ) = 0.2 ( x − 2 ) ( x + 1 ) ( x − 5 ) , express the function as a polynomial in general form and determine the leading term, degree, and end behavior of the function.
Identifying Local Behavior of Polynomial Functions
In addition to the end behavior of polynomial functions, we are also interested in what happens in the “middle” of the function. In particular, we are interested in locations where graph behavior changes. A turning point is a point at which the function values change from increasing to decreasing or decreasing to increasing.
We are also interested in the intercepts. As with all functions, the y- intercept is the point at which the graph intersects the vertical axis. The point corresponds to the coordinate pair in which the input value is zero. Because a polynomial is a function, only one output value corresponds to each input value so there can be only one y- intercept ( 0 , a 0 ) . ( 0 , a 0 ) . The x- intercepts occur at the input values that correspond to an output value of zero. It is possible to have more than one x- intercept. See Figure 9 .
Intercepts and Turning Points of Polynomial Functions
A turning point of a graph is a point at which the graph changes direction from increasing to decreasing or decreasing to increasing. The y- intercept is the point at which the function has an input value of zero. The x -intercepts are the points at which the output value is zero.
Given a polynomial function, determine the intercepts.
- Determine the y- intercept by setting x = 0 x = 0 and finding the corresponding output value.
- Determine the x -intercepts by solving for the input values that yield an output value of zero.
Determining the Intercepts of a Polynomial Function
Given the polynomial function f ( x ) = ( x − 2 ) ( x + 1 ) ( x − 4 ) , f ( x ) = ( x − 2 ) ( x + 1 ) ( x − 4 ) , written in factored form for your convenience, determine the y - and x -intercepts.
The y- intercept occurs when the input is zero so substitute 0 for x . x .
The y- intercept is (0, 8).
The x -intercepts occur when the output is zero.
The x -intercepts are ( 2 , 0 ) , ( – 1 , 0 ) , ( 2 , 0 ) , ( – 1 , 0 ) , and ( 4 , 0 ) . ( 4 , 0 ) .
We can see these intercepts on the graph of the function shown in Figure 10 .
Determining the Intercepts of a Polynomial Function with Factoring
Given the polynomial function f ( x ) = x 4 − 4 x 2 − 45 , f ( x ) = x 4 − 4 x 2 − 45 , determine the y - and x -intercepts.
The y- intercept occurs when the input is zero.
The y- intercept is ( 0 , −45 ) . ( 0 , −45 ) .
The x -intercepts occur when the output is zero. To determine when the output is zero, we will need to factor the polynomial.
The x -intercepts are ( 3 , 0 ) ( 3 , 0 ) and ( –3 , 0 ) . ( –3 , 0 ) .
We can see these intercepts on the graph of the function shown in Figure 11 . We can see that the function is even because f ( x ) = f ( − x ) . f ( x ) = f ( − x ) .
Given the polynomial function f ( x ) = 2 x 3 − 6 x 2 − 20 x , f ( x ) = 2 x 3 − 6 x 2 − 20 x , determine the y - and x -intercepts.
Comparing Smooth and Continuous Graphs
The degree of a polynomial function helps us to determine the number of x -intercepts and the number of turning points. A polynomial function of n th n th degree is the product of n n factors, so it will have at most n n roots or zeros, or x -intercepts. The graph of the polynomial function of degree n n must have at most n – 1 n – 1 turning points. This means the graph has at most one fewer turning point than the degree of the polynomial or one fewer than the number of factors.
A continuous function has no breaks in its graph: the graph can be drawn without lifting the pen from the paper. A smooth curve is a graph that has no sharp corners. The turning points of a smooth graph must always occur at rounded curves. The graphs of polynomial functions are both continuous and smooth.
Intercepts and Turning Points of Polynomials
A polynomial of degree n n will have, at most, n n x -intercepts and n − 1 n − 1 turning points.

Determining the Number of Intercepts and Turning Points of a Polynomial
Without graphing the function, determine the local behavior of the function by finding the maximum number of x -intercepts and turning points for f ( x ) = − 3 x 10 + 4 x 7 − x 4 + 2 x 3 . f ( x ) = − 3 x 10 + 4 x 7 − x 4 + 2 x 3 .
The polynomial has a degree of 10 , 10 , so there are at most 10 x -intercepts and at most 9 turning points.
Without graphing the function, determine the maximum number of x -intercepts and turning points for f ( x ) = 108 − 13 x 9 − 8 x 4 + 14 x 12 + 2 x 3 . f ( x ) = 108 − 13 x 9 − 8 x 4 + 14 x 12 + 2 x 3 .
Drawing Conclusions about a Polynomial Function from the Graph
What can we conclude about the polynomial represented by the graph shown in Figure 12 based on its intercepts and turning points?
The end behavior of the graph tells us this is the graph of an even-degree polynomial. See Figure 13 .
The graph has 2 x -intercepts, suggesting a degree of 2 or greater, and 3 turning points, suggesting a degree of 4 or greater. Based on this, it would be reasonable to conclude that the degree is even and at least 4.
What can we conclude about the polynomial represented by the graph shown in Figure 14 based on its intercepts and turning points?
Drawing Conclusions about a Polynomial Function from the Factors
Given the function f ( x ) = − 4 x ( x + 3 ) ( x − 4 ) , f ( x ) = − 4 x ( x + 3 ) ( x − 4 ) , determine the local behavior.
The y -intercept is found by evaluating f ( 0 ) . f ( 0 ) .
The y -intercept is ( 0 , 0 ) . ( 0 , 0 ) .
The x -intercepts are found by determining the zeros of the function.
The x -intercepts are ( 0 , 0 ) , ( –3 , 0 ) , ( 0 , 0 ) , ( –3 , 0 ) , and ( 4 , 0 ) . ( 4 , 0 ) .
The degree is 3 so the graph has at most 2 turning points.
Given the function f ( x ) = 0.2 ( x − 2 ) ( x + 1 ) ( x − 5 ) , f ( x ) = 0.2 ( x − 2 ) ( x + 1 ) ( x − 5 ) , determine the local behavior.
Access these online resources for additional instruction and practice with power and polynomial functions.
- Find Key Information about a Given Polynomial Function
- End Behavior of a Polynomial Function
- Turning Points and x - x - intercepts of Polynomial Functions
- Least Possible Degree of a Polynomial Function
5.2 Section Exercises
Explain the difference between the coefficient of a power function and its degree.
If a polynomial function is in factored form, what would be a good first step in order to determine the degree of the function?
In general, explain the end behavior of a power function with odd degree if the leading coefficient is positive.
What is the relationship between the degree of a polynomial function and the maximum number of turning points in its graph?
What can we conclude if, in general, the graph of a polynomial function exhibits the following end behavior? As x → − ∞ , f ( x ) → − ∞ x → − ∞ , f ( x ) → − ∞ and as x → ∞ , f ( x ) → − ∞ . x → ∞ , f ( x ) → − ∞ .
For the following exercises, identify the function as a power function, a polynomial function, or neither.
f ( x ) = x 5 f ( x ) = x 5
f ( x ) = ( x 2 ) 3 f ( x ) = ( x 2 ) 3
f ( x ) = x − x 4 f ( x ) = x − x 4
f ( x ) = x 2 x 2 − 1 f ( x ) = x 2 x 2 − 1
f ( x ) = 2 x ( x + 2 ) ( x − 1 ) 2 f ( x ) = 2 x ( x + 2 ) ( x − 1 ) 2
f ( x ) = 3 x + 1 f ( x ) = 3 x + 1
For the following exercises, find the degree and leading coefficient for the given polynomial.
− 3 x 4 − 3 x 4
7 − 2 x 2 7 − 2 x 2
− 2 x 2 − 3 x 5 + x − 6 − 2 x 2 − 3 x 5 + x − 6
x ( 4 − x 2 ) ( 2 x + 1 ) x ( 4 − x 2 ) ( 2 x + 1 )
x 2 ( 2 x − 3 ) 2 x 2 ( 2 x − 3 ) 2
For the following exercises, determine the end behavior of the functions.
f ( x ) = x 4 f ( x ) = x 4
f ( x ) = x 3 f ( x ) = x 3
f ( x ) = − x 4 f ( x ) = − x 4
f ( x ) = − x 9 f ( x ) = − x 9
f ( x ) = − 2 x 4 − 3 x 2 + x − 1 f ( x ) = − 2 x 4 − 3 x 2 + x − 1
f ( x ) = 3 x 2 + x − 2 f ( x ) = 3 x 2 + x − 2
f ( x ) = x 2 ( 2 x 3 − x + 1 ) f ( x ) = x 2 ( 2 x 3 − x + 1 )
f ( x ) = ( 2 − x ) 7 f ( x ) = ( 2 − x ) 7
For the following exercises, find the intercepts of the functions.
f ( t ) = 2 ( t − 1 ) ( t + 2 ) ( t − 3 ) f ( t ) = 2 ( t − 1 ) ( t + 2 ) ( t − 3 )
g ( n ) = −2 ( 3 n − 1 ) ( 2 n + 1 ) g ( n ) = −2 ( 3 n − 1 ) ( 2 n + 1 )
f ( x ) = x 4 − 16 f ( x ) = x 4 − 16
f ( x ) = x 3 + 27 f ( x ) = x 3 + 27
f ( x ) = x ( x 2 − 2 x − 8 ) f ( x ) = x ( x 2 − 2 x − 8 )
f ( x ) = ( x + 3 ) ( 4 x 2 − 1 ) f ( x ) = ( x + 3 ) ( 4 x 2 − 1 )
For the following exercises, determine the least possible degree of the polynomial function shown.
For the following exercises, determine whether the graph of the function provided is a graph of a polynomial function. If so, determine the number of turning points and the least possible degree for the function.
For the following exercises, make a table to confirm the end behavior of the function.
f ( x ) = − x 3 f ( x ) = − x 3
f ( x ) = x 4 − 5 x 2 f ( x ) = x 4 − 5 x 2
f ( x ) = x 2 ( 1 − x ) 2 f ( x ) = x 2 ( 1 − x ) 2
f ( x ) = ( x − 1 ) ( x − 2 ) ( 3 − x ) f ( x ) = ( x − 1 ) ( x − 2 ) ( 3 − x )
f ( x ) = x 5 10 − x 4 f ( x ) = x 5 10 − x 4
For the following exercises, graph the polynomial functions using a calculator. Based on the graph, determine the intercepts and the end behavior.
f ( x ) = x 3 ( x − 2 ) f ( x ) = x 3 ( x − 2 )
f ( x ) = x ( x − 3 ) ( x + 3 ) f ( x ) = x ( x − 3 ) ( x + 3 )
f ( x ) = x ( 14 − 2 x ) ( 10 − 2 x ) f ( x ) = x ( 14 − 2 x ) ( 10 − 2 x )
f ( x ) = x ( 14 − 2 x ) ( 10 − 2 x ) 2 f ( x ) = x ( 14 − 2 x ) ( 10 − 2 x ) 2
f ( x ) = x 3 − 16 x f ( x ) = x 3 − 16 x
f ( x ) = x 3 − 27 f ( x ) = x 3 − 27
f ( x ) = x 4 − 81 f ( x ) = x 4 − 81
f ( x ) = − x 3 + x 2 + 2 x f ( x ) = − x 3 + x 2 + 2 x
f ( x ) = x 3 − 2 x 2 − 15 x f ( x ) = x 3 − 2 x 2 − 15 x
f ( x ) = x 3 − 0.01 x f ( x ) = x 3 − 0.01 x
For the following exercises, use the information about the graph of a polynomial function to determine the function. Assume the leading coefficient is 1 or –1. There may be more than one correct answer.
The y - y - intercept is ( 0 , − 4 ) . ( 0 , − 4 ) . The x - x - intercepts are ( − 2 , 0 ) ( − 2 , 0 ) , ( 2 , 0 ) . ( 2 , 0 ) . Degree is 2.
End behavior: as x → − ∞ x → − ∞ , f ( x ) → ∞ f ( x ) → ∞ ; as x → ∞ x → ∞ , f ( x ) → ∞ . f ( x ) → ∞ .
The y - y - intercept is ( 0 , 9 ) . ( 0 , 9 ) . The x - x - intercepts are ( − 3 , 0 ) ( − 3 , 0 ) , ( 3 , 0 ) . ( 3 , 0 ) . Degree is 2.
End behavior: as x → − ∞ x → − ∞ , f ( x ) → − ∞ f ( x ) → − ∞ , as x → ∞ x → ∞ , f ( x ) → − ∞ . f ( x ) → − ∞ .
The y - y - intercept is ( 0 , 0 ) . ( 0 , 0 ) . The x - x - intercepts are ( 0 , 0 ) ( 0 , 0 ) , ( 2 , 0 ) . ( 2 , 0 ) . Degree is 3.
End behavior: as x → − ∞ x → − ∞ , f ( x ) → − ∞ f ( x ) → − ∞ , as x → ∞ x → ∞ , f ( x ) → ∞ . f ( x ) → ∞ .
The y - y - intercept is ( 0 , 1 ) . ( 0 , 1 ) . The x - x - intercept is ( 1 , 0 ) . ( 1 , 0 ) . Degree is 3.
End behavior: as x → − ∞ x → − ∞ , f ( x ) → ∞ f ( x ) → ∞ , as x → ∞ x → ∞ , f ( x ) → − ∞ . f ( x ) → − ∞ .
The y - y - intercept is ( 0 , 1 ) . ( 0 , 1 ) . There is no x - x - intercept. Degree is 4.
End behavior: as x → − ∞ x → − ∞ , f ( x ) → ∞ f ( x ) → ∞ , as x → ∞ x → ∞ , f ( x ) → ∞ . f ( x ) → ∞ .
Real-World Applications
For the following exercises, use the written statements to construct a polynomial function that represents the required information.
An oil slick is expanding as a circle. The radius of the circle is increasing at the rate of 20 meters per day. Express the area of the circle as a function of d , d , the number of days elapsed.
A cube has an edge of 3 feet. The edge is increasing at the rate of 2 feet per minute. Express the volume of the cube as a function of m , m , the number of minutes elapsed.
A rectangle has a length of 10 inches and a width of 6 inches. If the length is increased by x x inches and the width increased by twice that amount, express the area of the rectangle as a function of x . x .
An open box is to be constructed by cutting out square corners of x - x - inch sides from a piece of cardboard 8 inches by 8 inches and then folding up the sides. Express the volume of the box as a function of x . x .
A rectangle is twice as long as it is wide. Squares of side 2 feet are cut out from each corner. Then the sides are folded up to make an open box. Express the volume of the box as a function of the width ( x x ).
As an Amazon Associate we earn from qualifying purchases.
This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.
Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute OpenStax.
Access for free at https://openstax.org/books/college-algebra-2e/pages/1-introduction-to-prerequisites
- Authors: Jay Abramson
- Publisher/website: OpenStax
- Book title: College Algebra 2e
- Publication date: Dec 21, 2021
- Location: Houston, Texas
- Book URL: https://openstax.org/books/college-algebra-2e/pages/1-introduction-to-prerequisites
- Section URL: https://openstax.org/books/college-algebra-2e/pages/5-2-power-functions-and-polynomial-functions
© Jan 9, 2024 OpenStax. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License . The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

Describe the end behavior of the function - Explain and Show Work
2 answers by expert tutors.

Kenneth S. answered • 08/20/16
Algebra II EXPERT will help you survive & prosper

Neal D. answered • 08/20/16
Education Made Understandable
Still looking for help? Get the right answer, fast.
Get a free answer to a quick problem. Most questions answered within 4 hours.
Choose an expert and meet online. No packages or subscriptions, pay only for the time you need.
RELATED TOPICS
Related questions, finding rectangular equations from parametric equations.
Answers · 3
z+7/8 = z+8/9
Answers · 4
FOSSIL FUELS
Answers · 1
3x-6y/2x+6y * x^2+5xy+6y^2/6x^2-24y^2
Answers · 2
Solve for (x+y)^3
Recommended tutors.

find an online tutor
- Algebra 2 tutors
- Algebra 1 tutors
- PTCB tutors
- College Algebra tutors
- Hesi tutors
- CBEST tutors
- ISEE tutors
- FPGEE tutors
related lessons
- Algebra Worksheets List
- Algebra Study Tips
- Algebra Calculators
- Basics of Algebra
- Algebra Lessons List
- Trigonometry / Algebra 2 Trig Help
- Algebraic and Geometric Patterns
- Prealgebra Math Help

In order to continue enjoying our site, we ask that you confirm your identity as a human. Thank you very much for your cooperation.
Module 9: Power and Polynomial Functions
End behavior of polynomial functions, learning outcomes.
- Identify polynomial functions.
- Identify the degree and leading coefficient of polynomial functions.
- Describe the end behavior of a polynomial function.
Identifying Polynomial Functions
An oil pipeline bursts in the Gulf of Mexico causing an oil slick in a roughly circular shape. The slick is currently 24 miles in radius, but that radius is increasing by 8 miles each week. We want to write a formula for the area covered by the oil slick by combining two functions. The radius r of the spill depends on the number of weeks w that have passed. This relationship is linear.
[latex]r\left(w\right)=24+8w[/latex]
We can combine this with the formula for the area A of a circle.
[latex]A\left(r\right)=\pi {r}^{2}[/latex]
Composing these functions gives a formula for the area in terms of weeks.
[latex]\begin{array}{l}A\left(w\right)=A\left(r\left(w\right)\right)\\ A\left(w\right)=A\left(24+8w\right)\\ A\left(w\right)=\pi {\left(24+8w\right)}^{2}\end{array}[/latex]
Multiplying gives the formula below.
[latex]A\left(w\right)=576\pi +384\pi w+64\pi {w}^{2}[/latex]
This formula is an example of a polynomial function . A polynomial function consists of either zero or the sum of a finite number of non-zero terms, each of which is a product of a number, called the coefficient of the term, and a variable raised to a non-negative integer power.
A General Note: Polynomial Functions
Let n be a non-negative integer. A polynomial function is a function that can be written in the form
[latex]f\left(x\right)={a}_{n}{x}^{n}+\dots+{a}_{2}{x}^{2}+{a}_{1}x+{a}_{0}[/latex]
This is called the general form of a polynomial function. Each [latex]{a}_{i}[/latex] is a coefficient and can be any real number. Each product [latex]{a}_{i}{x}^{i}[/latex] is a term of a polynomial function .
Example: Identifying Polynomial Functions
Which of the following are polynomial functions?
[latex]\begin{array}{c}f\left(x\right)=2{x}^{3}\cdot 3x+4\hfill \\ g\left(x\right)=-x\left({x}^{2}-4\right)\hfill \\ h\left(x\right)=5\sqrt{x}+2\hfill \end{array}[/latex]
The first two functions are examples of polynomial functions because they can be written in the form [latex]f\left(x\right)={a}_{n}{x}^{n}+\dots+{a}_{2}{x}^{2}+{a}_{1}x+{a}_{0}[/latex], where the powers are non-negative integers and the coefficients are real numbers.
- [latex]f\left(x\right)[/latex] can be written as [latex]f\left(x\right)=6{x}^{4}+4[/latex].
- [latex]g\left(x\right)[/latex] can be written as [latex]g\left(x\right)=-{x}^{3}+4x[/latex].
- [latex]h\left(x\right)[/latex] cannot be written in this form and is therefore not a polynomial function.
Defining the Degree and Leading Coefficient of a Polynomial Function
Because of the form of a polynomial function, we can see an infinite variety in the number of terms and the power of the variable. Although the order of the terms in the polynomial function is not important for performing operations, we typically arrange the terms in descending order based on the power on the variable. This is called writing a polynomial in general or standard form. The degree of the polynomial is the highest power of the variable that occurs in the polynomial; it is the power of the first variable if the function is in general form. The leading term is the term containing the variable with the highest power, also called the term with the highest degree. The leading coefficient is the coefficient of the leading term.
A General Note: Terminology of Polynomial Functions

We often rearrange polynomials so that the powers on the variable are descending.
When a polynomial is written in this way, we say that it is in general form.
How To: Given a polynomial function, identify the degree and leading coefficient
- Find the highest power of x to determine the degree of the function.
- Identify the term containing the highest power of x to find the leading term.
- The leading coefficient is the coefficient of the leading term.
Example: Identifying the Degree and Leading Coefficient of a Polynomial Function
Identify the degree, leading term, and leading coefficient of the following polynomial functions.
[latex]\begin{array}{l} f\left(x\right)=3+2{x}^{2}-4{x}^{3} \\g\left(t\right)=5{t}^{5}-2{t}^{3}+7t\\h\left(p\right)=6p-{p}^{3}-2\end{array}[/latex]
For the function [latex]f\left(x\right)[/latex], the highest power of x is 3, so the degree is 3. The leading term is the term containing that degree, [latex]-4{x}^{3}[/latex]. The leading coefficient is the coefficient of that term, [latex]–4[/latex].
For the function [latex]g\left(t\right)[/latex], the highest power of t is 5, so the degree is 5. The leading term is the term containing that degree, [latex]5{t}^{5}[/latex]. The leading coefficient is the coefficient of that term, 5.
For the function [latex]h\left(p\right)[/latex], the highest power of p is 3, so the degree is 3. The leading term is the term containing that degree, [latex]-{p}^{3}[/latex]; the leading coefficient is the coefficient of that term, [latex]–1[/latex].
Identify the degree, leading term, and leading coefficient of the polynomial [latex]f\left(x\right)=4{x}^{2}-{x}^{6}+2x - 6[/latex].
The degree is 6. The leading term is [latex]-{x}^{6}[/latex]. The leading coefficient is [latex]–1[/latex].
In the following video, we show more examples of how to determine the degree, leading term, and leading coefficient of a polynomial.
Identifying End Behavior of Polynomial Functions
Knowing the leading coefficient and degree of a polynomial function is useful when predicting its end behavior. To determine its end behavior, look at the leading term of the polynomial function. Because the power of the leading term is the highest, that term will grow significantly faster than the other terms as x gets very large or very small, so its behavior will dominate the graph. For any polynomial, the end behavior of the polynomial will match the end behavior of the term of highest degree.
| Polynomial Function | Leading Term | Graph of Polynomial Function |
|---|---|---|
| [latex]f\left(x\right)=5{x}^{4}+2{x}^{3}-x - 4[/latex] | [latex]5{x}^{4}[/latex] | |
| [latex]f\left(x\right)=-2{x}^{6}-{x}^{5}+3{x}^{4}+{x}^{3}[/latex] | [latex]-2{x}^{6}[/latex] | |
| [latex]f\left(x\right)=3{x}^{5}-4{x}^{4}+2{x}^{2}+1[/latex] | [latex]3{x}^{5}[/latex] | |
| [latex]f\left(x\right)=-6{x}^{3}+7{x}^{2}+3x+1[/latex] | [latex]-6{x}^{3}[/latex] |
Example: Identifying End Behavior and Degree of a Polynomial Function
Describe the end behavior and determine a possible degree of the polynomial function in the graph below.
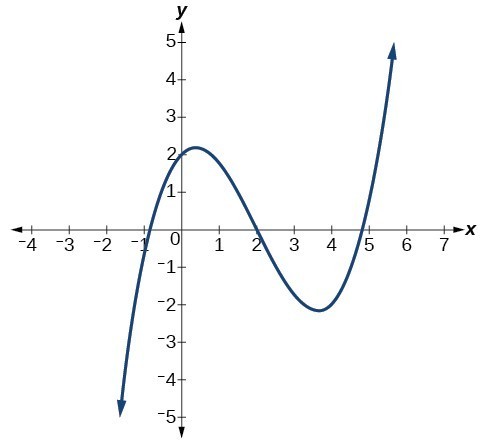
As the input values x get very large, the output values [latex]f\left(x\right)[/latex] increase without bound. As the input values x get very small, the output values [latex]f\left(x\right)[/latex] decrease without bound. We can describe the end behavior symbolically by writing
[latex]\begin{array}{c}\text{as } x\to -\infty , f\left(x\right)\to -\infty \\ \text{as } x\to \infty , f\left(x\right)\to \infty \end{array}[/latex]
In words, we could say that as x values approach infinity, the function values approach infinity, and as x values approach negative infinity, the function values approach negative infinity.
We can tell this graph has the shape of an odd degree power function that has not been reflected, so the degree of the polynomial creating this graph must be odd and the leading coefficient must be positive.
In the following video, we show more examples that summarize the end behavior of polynomial functions and which components of the function contribute to it.
Describe the end behavior of the polynomial function in the graph below.

As [latex]x\to \infty , f\left(x\right)\to -\infty[/latex] and as [latex]x\to -\infty , f\left(x\right)\to -\infty [/latex]. It has the shape of an even degree power function with a negative coefficient.
Given the function [latex]f\left(x\right)=-3{x}^{2}\left(x - 1\right)\left(x+4\right)[/latex], express the function as a polynomial in general form and determine the leading term, degree, and end behavior of the function.
Obtain the general form by expanding the given expression [latex]f\left(x\right)[/latex].
[latex]\begin{array}{l} f\left(x\right)=-3{x}^{2}\left(x - 1\right)\left(x+4\right)\\ f\left(x\right)=-3{x}^{2}\left({x}^{2}+3x - 4\right)\\ f\left(x\right)=-3{x}^{4}-9{x}^{3}+12{x}^{2}\end{array}[/latex]
The general form is [latex]f\left(x\right)=-3{x}^{4}-9{x}^{3}+12{x}^{2}[/latex]. The leading term is [latex]-3{x}^{4}[/latex]; therefore, the degree of the polynomial is 4. The degree is even (4) and the leading coefficient is negative (–3), so the end behavior is
[latex]\begin{array}{c}\text{as } x\to -\infty , f\left(x\right)\to -\infty \\ \text{as } x\to \infty , f\left(x\right)\to -\infty \end{array}[/latex]
Given the function [latex]f\left(x\right)=0.2\left(x - 2\right)\left(x+1\right)\left(x - 5\right)[/latex], express the function as a polynomial in general form and determine the leading term, degree, and end behavior of the function.
The leading term is [latex]0.2{x}^{3}[/latex], so it is a degree 3 polynomial. As x approaches positive infinity, [latex]f\left(x\right)[/latex] increases without bound; as x approaches negative infinity, [latex]f\left(x\right)[/latex] decreases without bound.
Number Line
- end\:behavior\:y=\frac{x^2+x+1}{x}
- end\:behavior\:f(x)=x^3
- end\:behavior\:f(x)=\ln(x-5)
- end\:behavior\:f(x)=\frac{1}{x^2}
- end\:behavior\:y=\frac{x}{x^2-6x+8}
- end\:behavior\:f(x)=\sqrt{x+3}
function-end-behavior-calculator
- Functions A function basically relates an input to an output, there’s an input, a relationship and an output. For every input...
Please add a message.
Message received. Thanks for the feedback.

IMAGES
VIDEO
COMMENTS
In general, the end behavior of a polynomial function is the same as the end behavior of its leading term, or the term with the largest exponent. So the end behavior of () = − x + is the same as the end behavior of the monomial − x . Since the degree of x is even () and the leading coefficient is negative () , the end ...
Describe the end behavior of each function. 1) f (x) = x3 − 4x2 + 7 2) f (x) = x3 − 4x2 + 4 3) f (x) = x3 − 9x2 + 24 x − 15 4) f (x) = x2 − 6x + 11 5) f (x) = x5 − 4x3 + 5x + 2 6) f (x) = −x2 + 4x 7) f (x) = 2x2 + 12 x + 12 8) f (x) = x2 − 8x + 18 State the maximum number of turns the graph of each function could make.
Algebra 2. Course: Algebra 2 ... Consider the polynomial function p (x) = − 9 x 9 + 6 x 6 − 3 x 3 + 1 . What is the end behavior of the graph of p ...
End behavior describes where a function is going at the extremes of the x-axis. In this video we learn the Algebra 2 way of describing those little arrows yo...
The end behavior of a polynomial function describes what happens to the outputs as the inputs are really small, or really large. ... we can describe the end behavior on the left as "going up." ... Look at how the graph of each function behaves in quadrants 2 and 3. In quadrants 2 and 3, x is always negative, and x is the input. ...
To determine its end behavior, look at the leading term of the polynomial function. Because the power of the leading term is the highest, that term will grow significantly faster than the other terms as x gets very large or very small, so its behavior will dominate the graph. For any polynomial, the end behavior of the polynomial will match the ...
Function f (x) is periodic if and only if: f (x + P) = f (x) Where P is a nonzero constant (commonly referred to as the fundamental period). A periodic function is basically a function that repeats after certain gap like waves. For example, the cosine and sine functions (i.e. f (x) = cos (x) and f (x) = sin (x)) are both periodic since their ...
2.2 End Behavior of Polynomials 1.Give the end behavior of the following functions: a. 4 : P ;3 P 8 ... F1 5 6 : T F3 ; 5 7 2. Create a polynomial function that satisfies the given criteria: the left and right end behavior is the same ... 3.Write the letter of the graph that corresponds with each equation on the line above the equation. ...
Correct answer: End Behavior: As x → −∞, y → −∞ and as x → ∞, y → ∞. Local maxima and minima: (0, 1) and (2, -3) Symmetry: Neither even nor odd. Explanation: To get started on this problem, it helps to use a graphing calculator or other graphing tool to visualize the function. The graph of y = x3 − 3x2 + 1 is below:
To predict the end-behavior of a polynomial function, first check whether the function is odd-degree or even-degree function and whether the leading coefficient is positive or negative. Find the end behavior of the function x 4 − 4 x 3 + 3 x + 25 . The degree of the function is even and the leading coefficient is positive. So, the end ...
1) f(x) = -5<6 + + 2 2) f(x) = + 2x3 -5<-6 CP A2 Unit 3 (chapter 6) Notes rd rd min i 51514 all relative minimums and maximums (rounded to 3 decimal places). Quick Check: Describe the end behavior of the graph of each polynomial function by completing the statements and s Ex 2: Graph the equation —5x+5 in your calculator.
2.2 Corrective Assignment. Are the following functions Polynomial Functions? If they are not, explain why. If they are, give the degree of the function. 2. Give the leading coefficient, the degree and the end behavior (if possible). 5. 9 3 6. 8. 37. 3 9.
Introduction to Systems of Equations and Inequalities; 7.1 Systems of Linear Equations: Two Variables; 7.2 Systems of Linear Equations: Three Variables; 7.3 Systems of Nonlinear Equations and Inequalities: Two Variables; 7.4 Partial Fractions; 7.5 Matrices and Matrix Operations; 7.6 Solving Systems with Gaussian Elimination; 7.7 Solving Systems with Inverses; 7.8 Solving Systems with Cramer's Rule
Describe the end behavior of the function - Explain and Show Work. f(x)=x^4 - x^3 - 2x^2 + 2. ... Trigonometry / Algebra 2 Trig Help; Algebraic and Geometric Patterns; Prealgebra Math Help; Download our free app. A link to the app was sent to your phone. Please provide a valid phone number.
The end behavior of a function f ( x) refers to how the function behaves when the variable x increases or decreases without bound. In other words, the end behavior describes the ultimate trend in ...
A polynomial function is a function that can be written in the form. f (x) =anxn +⋯+a2x2 +a1x+a0 f ( x) = a n x n + ⋯ + a 2 x 2 + a 1 x + a 0. This is called the general form of a polynomial function. Each ai a i is a coefficient and can be any real number. Each product aixi a i x i is a term of a polynomial function.
1st Edition • ISBN: 9781642088052 Laurie Boswell, Ron Larson. 5,286 solutions. 1 / 4. Find step-by-step Algebra 2 solutions and your answer to the following textbook question: Describe the end behavior of the graph of each function. $$ f ( x ) = - 5 x ^ { 4 } + 3 x ^ { 2 } $$.
Find step-by-step Algebra 2 solutions and your answer to the following textbook question: Describe the end behavior of each function. $$ c(a)=-a^2-2 a+22 $$.
Solution. The first two functions are examples of polynomial functions because they can be written in the form of Equation 5.2.2, where the powers are non-negative integers and the coefficients are real numbers. f(x) can be written as f(x) = 6x4 + 4. g(x) can be written as g(x) = − x3 + 4x.
The behavior of a function as \(x→±∞\) is called the function's end behavior. At each of the function's ends, the function could exhibit one of the following types of behavior: ... for \(f(x)=\dfrac{2+3e^x}{7−5e^x}\) and describe the end behavior of \(f.\) Solution. To find the limit as \(x→∞,\) divide the numerator and ...
Use an end behavior diagram (the ones shown in the discussion) to describe the end behavior of the graph of each function. Do not use a calculator. P (x) = − x − 3.2 x 3 + x 2 − 2.84 x 4 P(x)=-x-3.2 x^3+x^2-2.84 x^4 P (x) = − x − 3.2 x 3 + x 2 − 2.84 x 4
Algebra 2 Unit 5 Lesson 2 Homework Directions: For each graph, (a) Describe the end behavior, (b) Determin Get the answers you need, now! ... Degree of the Function: The described behavior suggests an odd-degree function as the ends show different trends. - (c) Sign of the Leading Coefficient: The leading coefficient is negative because the ...
Free Functions End Behavior calculator - find function end behavior step-by-step