Information
- Author Services

Initiatives
You are accessing a machine-readable page. In order to be human-readable, please install an RSS reader.
All articles published by MDPI are made immediately available worldwide under an open access license. No special permission is required to reuse all or part of the article published by MDPI, including figures and tables. For articles published under an open access Creative Common CC BY license, any part of the article may be reused without permission provided that the original article is clearly cited. For more information, please refer to https://www.mdpi.com/openaccess .
Feature papers represent the most advanced research with significant potential for high impact in the field. A Feature Paper should be a substantial original Article that involves several techniques or approaches, provides an outlook for future research directions and describes possible research applications.
Feature papers are submitted upon individual invitation or recommendation by the scientific editors and must receive positive feedback from the reviewers.
Editor’s Choice articles are based on recommendations by the scientific editors of MDPI journals from around the world. Editors select a small number of articles recently published in the journal that they believe will be particularly interesting to readers, or important in the respective research area. The aim is to provide a snapshot of some of the most exciting work published in the various research areas of the journal.
Original Submission Date Received: .
- Active Journals
- Find a Journal
- Proceedings Series
- For Authors
- For Reviewers
- For Editors
- For Librarians
- For Publishers
- For Societies
- For Conference Organizers
- Open Access Policy
- Institutional Open Access Program
- Special Issues Guidelines
- Editorial Process
- Research and Publication Ethics
- Article Processing Charges
- Testimonials
- Preprints.org
- SciProfiles
- Encyclopedia

Article Menu

- Subscribe SciFeed
- Recommended Articles
- Google Scholar
- on Google Scholar
- Table of Contents
Find support for a specific problem in the support section of our website.
Please let us know what you think of our products and services.
Visit our dedicated information section to learn more about MDPI.
JSmol Viewer
X-ray diffraction techniques for mineral characterization: a review for engineers of the fundamentals, applications, and research directions.

1. Introduction
2. crystal structure, 3. x-ray diffraction principle, 3.1. bragg’s law, 3.2. laue equations, 3.3. ewald theory, 4. applications of x-ray diffraction in mineral characterization, 4.1. phase identification and quantification, 4.2. lattice parameters, 4.3. crystalline structure, 4.4. crystal size and orientation, 4.5. phase transformation, 4.6. residual stress and strain, 4.7. dislocation density, 4.8. thermal expansion coefficient, 4.9. examples of xrd-characterized minerals and complementary techniques, 5. uncertainty, 5.1. constraints, 5.2. sources of error, 5.2.1. instrumental errors, 5.2.2. compositional variations errors, 5.3. detection limits, 5.4. quantification limits, 5.5. crystallinity, 6. safety considerations, 7. future research directions, 8. conclusions.
- These days, several mineral characterization operations including crystallite size measurement, residual stress and strain measurement within the crystal, determination of crystal structure, and others are conducted with sophisticated equipment and automated procedures.
- It was covered in the present review how Bragg’s theory provides practical utilization of XRD. Mineral crystal structure characterization significantly depends upon an accurate measurement of intensities and peak position of XRD patterns.
- The simplified mathematical model of Bragg’s theory made the capabilities of various XRD applications possible for measuring peak intensities and positions. In the characterization of minerals, it can be said that peak position influences unit cell parameters more as compared to peak intensity or peak width.
- XRD is still tackling the same questions since its embarkment over 100 years ago. Now we have the possibility to attach cooling and heating stages, and it is possible to make measurements with variations in temperature profiles and their effect on crystal parameters. Today, XRD equipment has become more user-friendly than ever, including portable equipment and smaller benchtop models.
- XRD possesses wide application areas, however, few complex crystal structures and diffraction patterns linked with crystal shape are still misunderstood. Hence, neither Laue’s nor Bragg’s theory can fully comprehend XRD patterns of complex crystal structures. More investigations are needed for a better understanding of intricate XRD patterns aimed for further improvements in mineral characterization.
- Other limitations of XRD applications include powdering of the sample as XRD works well with a powdered sample. It requires particle-size fractionation, milling, and careful sample splitting, which can be laborious. Due to the lack of contrast of peaks in the diffraction pattern and overlapping interference, XRD use is complicated as well. Moreover, sample preparation, K-value calculation, and drawing calibration curves are also intricate processes limiting the value of the XRD technique. Further research is needed for improving the overall XRD testing and analyses processes, especially for complex mineralogical structures.
- It was discussed how the use of deep and machine learning tools can aid the XRD technique to improve its accuracy and effectiveness. Furthermore, with the advent of these artificial intelligence techniques, it was also discussed how XRD technique can be pushed beyond its research frontiers, especially in the area of mineral characterization.
Author Contributions
Data availability statement, conflicts of interest, nomenclature.
| length of unit cell dimensions in directions, respectively | |
| Miller indices of crystallographic structure | |
| respective angles between unit cell dimensions in directions | |
| angles of incident and diffracted beams, respectively in direction | |
| angles of incident and diffracted beams, respectively in direction | |
| angles of incident and diffracted beams, respectively in direction | |
| X-ray wavelength | |
| unit vectors along the incident and diffracted beam directions, respectively | |
| unit vectors along the incident and diffracted beam directions, respectively, in the reciprocal lattice | |
| full width at half maximum | |
| instrument broadening | |
| size broadening | |
| strain broadening | |
| total broadening | |
| crystallographic directions | |
| crystallographic direction vector | |
| atomic distance between two adjacent atoms in space | |
| correspondence of wavelengths with integer numbers | |
| dislocation density | |
| lattice tensor | |
| Scherrer constant | |
| strain | |
| space distance | |
| reciprocal space distance | |
| particle size |
- Gilmore, C.J.; Kaduk, J.A.; Schenk., H. International Tables for Crystallography, Volume H: Powder Diffraction ; Wiley: Hoboken, NJ, USA, 2019. [ Google Scholar ]
- Cuéllar-Franca, R.M.; Azapagic, A. Carbon capture, storage and utilisation technologies: A critical analysis and comparison of their life cycle environmental impacts. J. CO 2 Util. 2015 , 9 , 82–102. [ Google Scholar ] [ CrossRef ]
- Gao, J.; Li, C.; Liu, W.; Hu, J.; Wang, L.; Liu, Q.; Liang, B.; Yue, H.; Zhang, G.; Luo, D.; et al. Process simulation and energy integration in the mineral carbonation of blast furnace slag. Chin. J. Chem. Eng. 2018 , 27 , 157–167. [ Google Scholar ] [ CrossRef ]
- Razeghi, M. Crystalline Properties of Solids. In Fundamentals of Solid State Engineering ; Kluwer Acad.: New York, NY, USA, 2002; pp. 1–43. [ Google Scholar ]
- Shackelford, J.F. Introduction to Materials Science for Engineers , 6th ed.; Pearson: London, UK, 2005. [ Google Scholar ]
- Bhadeshia, H.K.D.H. Teaching Materials. Available online: http://www.phase-trans.msm.cam.ac.uk/teaching.html (accessed on 4 October 2021).
- Sharma, R.; Bisen, D.P.; Shukla, U.; Sharma, B.G. X-RRY diffraction: A powerful method of characterizing nanomaterials. Recent Res. Sci. Technol. 2012 , 4 , 77–79. [ Google Scholar ]
- ICDD. PDF-4+ ; ICDD: Newtown Square, PA, USA, 2022. [ Google Scholar ]
- Pappas, N. Calculating retained austenite in steel post magnetic processing using X-ray diffraction. B. S. Undergr. Maths Exch. 2006 , 4 , 8–14. [ Google Scholar ]
- Guma, T.N.; Madakson, P.B.; Yawas, D.S.; Aku, S.Y. X-ray diffraction analysis of the microscopies of same corrosion protective bitumen coating. Int. J. Mod. Eng. Res. 2012 , 2 , 4387–4395. [ Google Scholar ]
- Hull, B.; John, V.B. Non-Destructive Testing ; Macmillan and Hound Mills Education Ltd.: Hampshire, UK, 1989. [ Google Scholar ]
- Hart, M. Bragg angle measurement and mapping. J. Cryst. Growth 1981 , 55 , 409–427. [ Google Scholar ] [ CrossRef ]
- Fewster, P.F. Absolute lattice parameter measurement. J. Mater. Sci. Mater. Electron. 1999 , 10 , 175–183. [ Google Scholar ] [ CrossRef ]
- Magner, S.H.; Angelis, R.J.O.; Weins, W.N.; Makinson, J.D. A historical review of retained austenite and its measurement by X-ray diffraction. Adv. X-ray Anal. 2002 , 45 , 85–97. [ Google Scholar ]
- Jesche, A.; Fix, M.; Kreyssig, A.; Meier, W.R.; Canfield, P.C. X-ray diffraction on large single crystals using a powder diffractometer. Philos. Mag. 2018 , 96 , 2115–2124. [ Google Scholar ] [ CrossRef ] [ Green Version ]
- Matsubara, E.; Shinoda, K.; Waseda, Y. X-ray Diffraction Crystallography: Introduction, Examples and Solved Problems ; Springer: Berlin/Heidelberg, Germany, 2011. [ Google Scholar ]
- Putnam, C.; Hammel, M.; Hura, G.L.; Tainer, J. X-ray solution scattering (saxs) combined with crystallography and computation: Defining accurate macromolecular structures, conformations and assembling in solution. Q. Rev. Biophys. 2007 , 40 , 191–285. [ Google Scholar ] [ CrossRef ] [ PubMed ]
- Dekker, A.J. The Crystalline State. In Solid State Physics ; MacMillan Co Ltd.: New York, NY, USA, 1952; pp. 1–31. [ Google Scholar ]
- Aroyo, M.I. International Tables for Crystallography Volume A: Space-Group Symmetry ; Wiley: Hoboken, NJ, USA, 2016. [ Google Scholar ]
- Wang, L.; Essin, A.; Hermele, M.; Motrunich, O. Numerical detection of symmetry-enriched topological phases with space-group symmetry. Phys. Rev. B 2015 , 91 , 121103. [ Google Scholar ] [ CrossRef ] [ Green Version ]
- Hu, S.Z.; Ng, S.W. Revisions of P-1 Space Groups to Higher Symmetry Space Groups. Chin. J. Struct. Chem. 2014 , 33 , 148–164. [ Google Scholar ]
- Palistrant, A.F. Using the P-symmetry space groups of crystals to investigate 6D symmetry groups. Crystallogr. Rep. 2009 , 54 , 539–547. [ Google Scholar ] [ CrossRef ]
- Hahn, T. Status of Volume A: Space-group Symmetry. ACTA Crystallogr. A—Found. Adv. 2005 , 61 , C132. [ Google Scholar ] [ CrossRef ]
- Mizutani, U.; Sato, H. The Physics of the Hume-Rothery Electron Concentration Rule. Crystals 2017 , 7 , 9. [ Google Scholar ] [ CrossRef ] [ Green Version ]
- Fultz, B.; Howe, J. Transmission Electron Microscopy and Diffractometry of Materials ; Springer: Berlin/Heidelberg, Germany, 2013. [ Google Scholar ]
- Lamas, D.G.; Neto, M.D.O.; Kellermann, G.; Craievich, A.F. X-ray Diffraction and Scattering by Nanomaterials. In Nanocharacterization Techniques ; William Andrew Publishing: Oxford, UK, 2017; Chapter 5; pp. 111–182. [ Google Scholar ]
- Sjöström, J.K.; Bindler, R.; Granberg, T.; Kylander, M.E. Procedure for Organic Matter Removal from Peat Samples for XRD Mineral Analysis. Wetlands 2019 , 39 , 473–481. [ Google Scholar ] [ CrossRef ] [ Green Version ]
- Lee, M. X-ray Diffraction for Materials Research from Fundamentals to Applications ; CRC Press: Boca Raton, FL, USA, 2021. [ Google Scholar ]
- Macías-Quiroga, I.F.; Giraldo-Gómez, G.I.; Sanabria-González, N.R. Characterization of Colombian Clay and Its Potential Use as Adsorbent. Sci. World J. 2018 , 2018 , 5969178. [ Google Scholar ] [ CrossRef ] [ Green Version ]
- Authier, A. Dynamical Theory of X-ray Diffraction ; Oxford University Press: Oxford, UK, 2001. [ Google Scholar ]
- Sivia, D.S. Elementary Scattering Theory for X-ray and Neutron Users ; Oxford University Press: New York, NY, USA, 2011. [ Google Scholar ]
- Ameh, E.S. A review of basic crystallography and X-ray diffraction applications. Int. J. Adv. Manuf. Technol. 2019 , 105 , 3289–3302. [ Google Scholar ] [ CrossRef ]
- Hammond, C. The Basics of Crystallography and Diffraction , 3rd ed.; Oxford University Press: Oxford, UK, 2009. [ Google Scholar ]
- Ashcroft, N.W.; Mernin, N.D. Solid State Physics ; Harcourt College Publishers: Fort Worth, TX, USA, 1976. [ Google Scholar ]
- Helliwell, J.R.; Blake, A.J.; Blunden-Ellis, J.; Moore, M.; Schwalbe, C.H. Some historical extracts relevant to the discovery and application of the diffraction of X-rays by crystals to contribute to the Centennial celebration and the International Year of Crystallography. Crystallogr. Rev. 2011 , 18 , 3–19. [ Google Scholar ] [ CrossRef ]
- Wood, E.A. Vocabulary of surface crystallography. J. Appl. Physiol. 1964 , 35 , 1306–1312. [ Google Scholar ] [ CrossRef ]
- Fewster, P.F. Response to Fraser & Wark’s comments on a new theory for X-ray diffraction. Acta Crystallogr. Sect. A 2018 , 74 , 457–465. [ Google Scholar ]
- Gilmore, C.J.; Barr, G.; Paisley, J. High throughput powder diffraction. A new approach to qualitative and quantitative powder diffraction pattern analysis using full pattern profile. J. Appl. Crystallogr. 2004 , 37 , 231–242. [ Google Scholar ] [ CrossRef ] [ Green Version ]
- Lou, W.; Zhang, D.; Bayless, R.C. Review of mineral recognition and its future. Appl. Geochem. 2020 , 122 , 104727. [ Google Scholar ] [ CrossRef ]
- Bish, D.L.; Plötze, M. X-ray Powder Diffraction with Emphasis on Qualitative and Quantitative Analysis in Industrial Min-eralogy. In Advances in the Characterization of Industrial Minerals ; European Mineralogical Union: London, UK, 2010. [ Google Scholar ]
- Ran, J.; Du, G.; Wang, F.Y. Rapid analysis of feldspar by X-ray diffractometry rietveld refinement method. Rock Miner. Anal. 2017 , 36 , 489–494. [ Google Scholar ]
- Wang, C.; Yang, R.; Wang, H. Synthesis of ZIF-8/Fly Ash Composite for Adsorption of Cu 2+ , Zn 2+ and Ni 2+ from Aqueous Solutions. Materials 2020 , 13 , 214. [ Google Scholar ] [ CrossRef ] [ Green Version ]
- Hamilton, J.; Wilson, S.; Turvey, C.; Morgan, B.; Tait, A.; McCutcheon, J.; Fallon, S.; Southam, G. Carbon accounting of mined landscapes, and deployment of a geochemical treatment system for enhanced weathering at Woodsreef Chrysotile Mine, NSW, Australia. J. Geochem. Explor. 2021 , 220 , 106655. [ Google Scholar ] [ CrossRef ]
- Rodríguez, I.; Gautam, R.; Tinoco, A. Using X-ray Diffraction Techniques for Biomimetic Drug Development, Formulation, and Polymorphic Characterization. Biomimetics 2021 , 6 , 1. [ Google Scholar ] [ CrossRef ]
- Haque, F.; Santos, R.M.; Chiang, Y.W. Optimizing Inorganic Carbon Sequestration and Crop Yield With Wollastonite Soil Amendment in a Microplot Study. Front. Plant Sci. 2020 , 11 , 1012. [ Google Scholar ] [ CrossRef ]
- Taylor, J.; Clapp, R. New Features and Advanced Applications of Siroquant: A Personal Computer XRD Full Profile Quantitative Analysis Software Package. Adv. X-ray Anal. 1991 , 35 , 49–55. [ Google Scholar ] [ CrossRef ]
- Walenta, C.; Fullmann, T. Advances in quantitative XRD analysis for clinker, cements, and cementitious additions. Int. Cent. Diffr. Data 2004 , 19 , 40–44. [ Google Scholar ] [ CrossRef ] [ Green Version ]
- Henry, N.F.M.; Lipson, H.; Wooster, W.A.; Cullity, B.D. The Interpretation of X-ray Diffraction Photographs ; Macmillian Ltd.: London, UK, 1961. [ Google Scholar ]
- Tilley, R. Understanding Solids: The Science of Materials ; John Wiley & Sons Ltd.: West Sussex, UK, 2004. [ Google Scholar ]
- Rietveld, H.M. The Rietveld method. Phys. Scr. 2014 , 89 , 098002. [ Google Scholar ] [ CrossRef ]
- Rojas-Mantilla, H.D.; Ayala-Duran, S.C.; Nogueira, R.F.P. Nontronite mineral clay NAu-2 as support for hematite applied as catalyst for heterogeneous photo-Fenton processes. Chemosphere 2021 , 277 , 130258. [ Google Scholar ] [ CrossRef ]
- Harris, W.; White, N. X-ray Chapter 4-Diffraction Techniques for Soil Mineral Identification. Methods Soil Anal. Part Mineral. Methods 2008 , 5 , 81–115. [ Google Scholar ]
- Jacob, R.; Nair, H.G.; Isac, J. Structural and morphological studies of nano-crystalline ceramic BaSr 0.9 Fe 0.1 TiO 4 . Int. Lett. Chem. Phys. Astron. 2015 , 41 , 100–117. [ Google Scholar ] [ CrossRef ] [ Green Version ]
- Barman, B.; Sarma, K.C. Structural characterization of PVA capped ZnS nano structured thin film. Indian J. Phys. 2010 , 86 , 703–707. [ Google Scholar ] [ CrossRef ]
- West, A.R. Solid State Chemistry and Its Application ; Wiley & Sons: New York, NY, USA, 1974. [ Google Scholar ]
- Artioli, G. Science for the cultural heritage: The contribution of X-ray diffraction. X-ray Diffr. 2013 , 24 , 55–62. [ Google Scholar ] [ CrossRef ]
- Cléton, F.; Jouneau, P.H.; Henry, S.; Gäumann, M.; Buffat, P.A. Crystallographic orientation assessment by electron backscattered diffraction. Scanning 1999 , 21 , 232–237. [ Google Scholar ] [ CrossRef ] [ Green Version ]
- Gräfe, M.; Klauber, C.; Gan, B.; Tappero, R.V. Synchrotron X-ray microdiffraction (μXRD) in minerals and environmental research. Powder Diffr. 2014 , 29 , 64–72. [ Google Scholar ] [ CrossRef ]
- Lekston, Z.; Zubko, M. X-ray diffraction studies of the reversible phase transformation in niti shape memory alloy. Acta Phys. Pol. A 2016 , 130 , 1059–1062. [ Google Scholar ] [ CrossRef ]
- Lamiri, I.; Martinez-Blanco, D.; Abdelbaky, M.S.; Mari, D.; Hamana, D.; Garcia-Granda, S. Investigation of the order -disorder phase transition series in AuCu by in-situ temperature XRD and mechanical spectroscopy. J. Alloys Compd. 2019 , 770 , 748–754. [ Google Scholar ] [ CrossRef ]
- McCormack, S.J.; Tseng, K.P.; Weber, R.J.; Kapush, D.; Ushakov, S.V.; Navrotsky, A.; Kriven, W.M. In Situ Determination of the HfO 2 -Ta 2 O 5 -Temperature Phase Diagram up to 3000 °C. J. Am. Ceram. Soc. 2018 , 102 , 4848–4861. [ Google Scholar ] [ CrossRef ]
- Malinov, S.; Sha, W.; Guo, Z.; Tang, C.; Long, A. Synchrotron X-ray diffraction study of the phase transformation in titanium alloys. Mater. Charact. 2002 , 48 , 279–295. [ Google Scholar ] [ CrossRef ] [ Green Version ]
- Ashiri, R.; Nemati, A.; Ghamsari, M.S.; Sanjabi, S.; Aalipour, M. A modified method for barium titanate nanoparticles synthesis. Mater. Res. Bull. 2011 , 46 , 2291–2295. [ Google Scholar ] [ CrossRef ]
- Bemporad, E.; Brisotto, M.; Depero, L.; Gelfi, M.; Korsunsky, A.; Lunt, A.; Sebastiani, M. A critical comparison between XRD and FIB residual stress measurement techniques in thin films. Thin Solid Films 2014 , 572 , 224–231. [ Google Scholar ] [ CrossRef ]
- Singh, J.; Ranwa, S.; Akhtar, J.; Kumar, M. Growth of residual stress-free ZnO films on SiO 2 /Si substrate at room temperature for MEMS devices. AIP Adv. 2015 , 5 , 067140. [ Google Scholar ] [ CrossRef ]
- Ungar, T. Strain broadening caused by dislocation. Mater. Sci. Forum 1994 , 923 , 166–169. [ Google Scholar ] [ CrossRef ]
- Weertman, J.R. Hall-Petch strengthening in nano crystalline metal. Mater. Sci. Eng. A 1993 , 166 , 161–167. [ Google Scholar ] [ CrossRef ]
- Subbaiah, Y.V.; Prathap, P.; Reddy, K.R. Structural, electrical and optical properties of ZnS film deposited by close-spaced evaporation. Appl. Surf. Sci. 2006 , 253 , 2409–2415. [ Google Scholar ] [ CrossRef ]
- Huang, C.-Y.; Hsu, Y.-C.; Chen, J.-G.; Suryanarayanan, V.; Lee, K.-M.; Ho, K.-C. The effects of hydrothermal temperature and thickness of TiO 2 film on the performance of a dye-sensitized solar cell. Sol. Energy Mater. Sol. Cells 2006 , 90 , 2391–2397. [ Google Scholar ] [ CrossRef ]
- Hummer, D.R.; Heaney, P.J.; Post, J.E. Thermal expansion of anatase and rutile between 300 and 575 K using synchrotron powder X-ray diffraction. Powder Diffr. 2007 , 22 , 352–356. [ Google Scholar ] [ CrossRef ]
- Nagash, S.; Gerhards, M.T.; Tietz, F.; Guillon, O. Coefficient of thermal expansion of Al- and Y-substituted NaSICON solid solution Na 3+2x Al x Y x Zr 2−2x Si 2 PO 12 . Batteries 2018 , 4 , 33. [ Google Scholar ] [ CrossRef ] [ Green Version ]
- Pathak, P.D.; Vasavada, N.G. Thermal expansion of NaCl, KCl and C S Br by X-ray diffraction and the law of corresponding states. Acta Crystallogr. Sect. A 1970 , 26 , 655–661. [ Google Scholar ] [ CrossRef ]
- Bouyrie, Y.; Candolfi, C.; Pailhès, S. From crystal to glass-like thermal conductivity in crystalline minerals. Phys. Chem. Chem. Phys. 2015 , 17 , 19751–19758. [ Google Scholar ] [ CrossRef ]
- Heidari, Z.; Pelalak, R.; Alizadeh, R.; Oturan, N.; Shirazian, S.; Oturan, M.A. Application of Mineral Iron-Based Natural Catalysts in Electro-Fenton Process: A Comparative Study. Catalysts 2021 , 11 , 57. [ Google Scholar ] [ CrossRef ]
- Bora, J.; Deka, P.; Bhuyan, P.; Sarma, K.P.; Hoque, R.R. Morphology and mineralogy of ambient particulate matter over mid-Brahmaputra Valley: Application of SEM–EDX, XRD, and FTIR techniques. SN Appl. Sci. 2021 , 3 , 137. [ Google Scholar ] [ CrossRef ]
- Mulenshi, J.; Gilbricht, S.; Chelgani, S.C.; Rosenkranz, J. Systematic characterization of historical tailings for possible remediation and recovery of critical metals and minerals—The Yxsjöberg case. J. Geochem. Explor. 2021 , 226 , 106777. [ Google Scholar ] [ CrossRef ]
- Gong, X.; Jiang, W.; Hu, S.; Yang, Z.; Liu, X.; Fan, Z. Comprehensive utilization of foundry dust: Coal powder and clay minerals separation by ultrasonic-assisted flotation. J. Hazard. Mater. 2021 , 402 , 124124. [ Google Scholar ] [ CrossRef ]
- Yuan, L.; Liu, Q.; Mathews, J.P.; Zhang, H.; Wu, Y. Quantifying the Structural Transitions of Chinese Coal to Coal-Derived Natural Graphite by XRD, Raman Spectroscopy, and HRTEM Image Analyses. Energy Fuels 2021 , 35 , 2335–2346. [ Google Scholar ] [ CrossRef ]
- Li, Q.; Zhang, L.; Gao, X.; Zhang, J. Effect of pulverized fuel ash, ground granulated blast-furnace slag and CO 2 curing on performance of magnesium oxysulfate cement. Constr. Build. Mater. 2019 , 230 , 116990. [ Google Scholar ] [ CrossRef ]
- Nergis, D.D.; Abdullah, M.M.A.B.; Sandu, A.V.; Vizureanu, P. XRD and TG-DTA Study of New Alkali Activated Materials Based on Fly Ash with Sand and Glass Powder. Materials 2020 , 13 , 343. [ Google Scholar ] [ CrossRef ] [ Green Version ]
- Zhang, X.; Ge, J.; Kamali, F.; Othman, F.; Wang, Y.; Le-Hussain, F. Wettability of sandstone rocks and their mineral components during CO 2 injection in aquifers: Implications for fines migration. J. Nat. Gas Sci. Eng. 2019 , 73 , 103050. [ Google Scholar ] [ CrossRef ]
- Song, Q.; Zhao, H.; Jia, J.; Yang, L.; Lv, W.; Gu, Q.; Shu, X. Effects of demineralization on the surface morphology, microcrystalline and thermal transformation characteristics of coal. J. Anal. Appl. Pyrolysis 2019 , 145 , 104716. [ Google Scholar ] [ CrossRef ]
- Jacob, S.R.; Wellington, D.F.; Bell, J.F.; Achilles, C.; Fraeman, A.A.; Horgan, B.; Johnson, J.R.; Maurice, S.; Peters, G.H.; Rampe, E.B.; et al. Spectral, Compositional, and Physical Properties of the Upper Murray Formation and Vera Rubin Ridge, Gale Crater, Mars. J. Geophys. Res. Planets 2020 , 125 , e2019JE006290. [ Google Scholar ] [ CrossRef ]
- Fang, S.; Xu, L.; Wu, H.; Xu, Y.; Wang, Z.; Shu, K.; Longhua, X. Influence of surface dissolution on sodium oleate adsorption on ilmenite and its gangue minerals by ultrasonic treatment. Appl. Surf. Sci. 2019 , 500 , 144038. [ Google Scholar ] [ CrossRef ]
- Fahad, M.; Ali, S.; Iqbal, Y. Plasma diagnostics by optical emission spectroscopy on manganese ore in conjunction with XRD, XRF and SEM-EDS. Plasma Sci. Technol. 2019 , 21 , 085507. [ Google Scholar ] [ CrossRef ]
- Idris, A.; El-Zahhar, A.A. Indicative properties measurements by SEM, SEM-EDX and XRD for initial homogeneity tests of new certified reference materials. Microchem. J. 2019 , 146 , 429–433. [ Google Scholar ] [ CrossRef ]
- Awadh, S.M.; Yaseen, Z.M. Investigation of silica polymorphs stratified in siliceous geode using FTIR and XRD methods. Mater. Chem. Phys. 2019 , 228 , 45–50. [ Google Scholar ] [ CrossRef ]
- Qin, L.; Gao, X.; Chen, T. Influence of mineral admixtures on carbonation curing of cement paste. Constr. Build. Mater. 2019 , 212 , 653–662. [ Google Scholar ] [ CrossRef ]
- Zhang, L.; Li, Y.; Guo, H.; Zhang, H.; Zhang, N.; Hayat, T.; Sun, Y. Decontamination of U(VI) on graphene oxide/Al 2 O 3 composites investigated by XRD, FT-IR and XPS techniques. Environ. Pollut. 2019 , 248 , 332–338. [ Google Scholar ] [ CrossRef ]
- Joni, I.M.; Nulhakim, L.; Vanitha, M.; Panatarani, C. Characteristics of crystalline silica (SiO 2 ) particles prepared by simple solution method using sodium silicate (Na 2 SiO 3 ) precursor. J. Phys. Conf. Ser. 2018 , 1080 , 012006. [ Google Scholar ] [ CrossRef ]
- Zhou, X.; Liu, D.; Bu, H.; Deng, L.; Liu, H.; Yuan, P.; Du, P.; Song, H. XRD-based quantitative analysis of clay minerals using reference intensity ratios, mineral intensity factors, Rietveld, and full pattern summation methods: A critical review. Solid Earth Sci. 2018 , 3 , 16–29. [ Google Scholar ] [ CrossRef ]
- Loganathan, N.; Bowers, G.M.; Yazaydin, A.O.; Schaef, H.T.; Loring, J.S.; Kalinichev, A.G.; Kirkpatrick, R.J. Clay Swelling in Dry Supercritical Carbon Dioxide: Effects of Interlayer Cations on the Structure, Dynamics, and Energetics of CO 2 Intercalation Probed by XRD, NMR, and GCMD Simulations. J. Phys. Chem. C 2018 , 122 , 4391–4402. [ Google Scholar ] [ CrossRef ] [ Green Version ]
- Sun, Z.; Vollpracht, A. Isothermal calorimetry and in-situ XRD study of the NaOH activated fly ash, metakaolin and slag. Cem. Concr. Res. 2018 , 103 , 110–122. [ Google Scholar ] [ CrossRef ]
- Hupp, B.N.; Donovan, J.J. Quantitative mineralogy for facies definition in the Marcellus Shale (Appalachian Basin, USA) using XRD-XRF integration. Sediment. Geol. 2018 , 371 , 16–31. [ Google Scholar ] [ CrossRef ]
- Li, Z.; Tang, L.; Zheng, Y.; Tian, D.; Su, M.; Zhang, F.; Ma, S.; Hu, S. Characterizing the Mechanisms of Lead Immobilization via Bioapatite and Various Clay Minerals. ACS Earth Space Chem. 2017 , 1 , 152–157. [ Google Scholar ] [ CrossRef ]
- Induja, I.; Sebastian, M. Microwave dielectric properties of mineral sillimanite obtained by conventional and cold sintering process. J. Eur. Ceram. Soc. 2017 , 37 , 2143–2147. [ Google Scholar ] [ CrossRef ] [ Green Version ]
- Khan, H.; Yerramilli, A.S.; D’Oliveira, A.; Alford, T.L.; Boffito, D.C.; Patience, G.S. Experimental methods in chemical engineering: X-ray diffraction spectroscopy-XRD. Can. J. Chem. Eng. 2020 , 98 , 1255–1266. [ Google Scholar ] [ CrossRef ]
- Awad, M.E.; López-Galindo, A.; Sánchez-Espejo, R.; Sainz-Díaz, C.I.; El-Rahmany, M.M.; Viseras, C. Crystallite size as a function of kaolinite structural order-disorder and kaolin chemical variability: Sedimentological implication. Appl. Clay Sci. 2018 , 162 , 261–267. [ Google Scholar ] [ CrossRef ]
- Silva, A.L.D.; Oliveira, A.H.D.; Fernandes, M.L.S. Influence of preferred orienation of minerals in the mineralogical identification process by X-ray diffraction. In Proceedings of the INAC 2011: International Nuclear Atlantic Conference, Belo Horizonte, MG, Brazil, 24–28 October 2011. [ Google Scholar ]
- Cullity, B.; Stock, S. Elements of X-ray Diffraction ; Pearson Education Limited: New Delhi, India, 2014. [ Google Scholar ]
- Hermann, H.; Ermrich, M. Microabsorption Correction of X-Ray Intensities Diffracted by Multiphase Powder Specimens. Powder Diffr. 1989 , 4 , 189–195. [ Google Scholar ] [ CrossRef ]
- Scarlett, N.V.Y.; Madsen, I.C.; Cranswick, L.M.D.; Lwin, T.; Groleau, E.; Stephenson, G.; Aylmore, M.; Agron-Olshinaa, N. Outcomes of the International Union of Crystallography Commission on Powder Diffraction Round Robin on Quantitative Phase Analysis: Samples 2, 3, 4, synthetic bauxite, natural granodiorite and pharmaceut. J. Appl. Crystallogr. 2002 , 35 , 383–400. [ Google Scholar ] [ CrossRef ]
- De Campos, M.F.; Machado, J.C.D.R.; Achete, C.A. Metrology for a Sustainable Development Brazil. In Proceedings of the XVIII IMEKO World Congress, Rio de Janeiro, Brazil, 17–22 September 2006. [ Google Scholar ]
- Igwebike-Ossi, C.D. X-ray Techniques. In Failure Analysis and Prevention ; IntechOpen: London, UK, 2017. [ Google Scholar ]
- Bish, D.L.; Reynolds, R.C. Sample Preparation for X-ray Diffraction. Mod. Powder Diffr. 2018 , 20 , 73–100. [ Google Scholar ]
- Rathnaweera, T.; Ranjith, P.; Gu, X.; Perera, S.; Kumari, W.; Wanniarachchi, A.; Haque, A.; Li, J. Experimental investigation of thermomechanical behaviour of clay-rich sandstone at extreme temperatures followed by cooling treatments. Int. J. Rock Mech. Min. Sci. 2018 , 107 , 208–223. [ Google Scholar ] [ CrossRef ]
- Garcia-Granada, G.; Montejo-Bernardo, J. X-ray Diffraction-Powder ; Reference Module in Chemistry Molecular Sciences and Chemical Engineering; Elsevier: Amsterdam, The Netherlands, 2013. [ Google Scholar ]
- Sarrazin, P.C.; Blake, D.F.; Gailhanou, M.; Chen, J.; Dera, P.; Downs, R.T.; Bristow, T.F. New Developments In X-ray Diffraction For Planetary Exploration. In Proceedings of the 49th Lunar and Planetary Science Conference, The Woodlands, TX, USA, 19–30 March 2018. [ Google Scholar ]
- Černý, R. Crystal Structures from Powder Diffraction: Principles, Difficulties and Progress. Crystals 2017 , 7 , 142. [ Google Scholar ] [ CrossRef ] [ Green Version ]
- Bergmann, J.; Le Bail, A.; Shirley, R.; Zlokazov, V. Renewed interest in powder diffraction data indexing. Z. Krist.—Cryst. Mater. 2004 , 219 , 783–790. [ Google Scholar ] [ CrossRef ]
- Fitch, A.; Curfs, C. Ultrafast Powder Diffraction. In The Power of Powder Diffraction ; Erice International School of Crystallography: Erice, Italy, 2011; pp. 103–112. [ Google Scholar ]
- Smrčok, L. Powder Diffraction + Computational Methods. In The Power of Powder Diffraction ; Erice International School of Crystallography: Erice, Italy, 2011; pp. 231–238. [ Google Scholar ]
- Suzuki, Y.; Hino, H.; Hawai, T.; Saito, K.; Kotsugi, M.; Ono, K. Symmetry prediction and knowledge discovery from X-ray diffraction patterns using an interpretable machine learning approach. Sci. Rep. 2020 , 10 , 21790. [ Google Scholar ] [ CrossRef ]
- Lee, J.-W.; Park, W.B.; Singh, S.P.; Sohn, K.-S. A deep-learning technique for phase identification in multiphase inorganic compounds using synthetic XRD powder patterns. Nat. Commun. 2020 , 11 , 86. [ Google Scholar ] [ CrossRef ] [ Green Version ]
- Ziletti, A.; Kumar, D.; Scheffler, M.; Ghiringhelli, L.M. Insightful classification of crystal structures using deep learning. Nat. Commun. 2018 , 9 , 2775. [ Google Scholar ] [ CrossRef ] [ Green Version ]
Click here to enlarge figure
| Techniques/Methods | Year | Minerals/Materials | Reference |
|---|---|---|---|
| XRD and Raman | 2021 | Ilmenite, pyrite, chromite, chalcopyrite | [ ] |
| XRD, FTIR, SEM-EDX | 2021 | Quartz, illite, augite, kaolinite, calcite etc. | [ ] |
| XRD, MLA | 2021 | Scheelite, fluorite, pyrrhotite, pyrite | [ ] |
| XRD, XRF, EPMA | 2021 | Clay minerals | [ ] |
| XRD, Raman Spectroscopy, HRTEM | 2021 | Coal, graphite | [ ] |
| XRD, FTIR, SEM, TG-DTA, SEM-EDS | 2020 | Pulverized fuel ash, slag, magnesium oxysulfate cement | [ ] |
| XRD, TG-DTA | 2020 | Fly ash with sand and glass powder | [ ] |
| XRD, XRF, SEM-EDS | 2020 | Sandstones and their mineral components | [ ] |
| XRD, FTIR, SEM, AFM, TGA, GC | 2020 | Raw coal and acid washing coal | [ ] |
| XRD | 2020 | Upper Murray formation, Vera Rubin Ridge, Gale Crater | [ ] |
| XRD, XPS, ICP-OES | 2020 | Ilmenite, titanaugite, olivine | [ ] |
| XRD, XRF, SEM-EDS | 2019 | Manganese | [ ] |
| XRD, SEM, SEM-EDX | 2019 | Certified reference materials including soil, dust, sediment, leaves, dates, and fish | [ ] |
| XRD, FTIR | 2019 | Silica polymorphs | [ ] |
| XRD, FTIR, TG-DTA, MIP, SEM | 2019 | Ground granulated blast-furnace slag, fly ash, cement mortars | [ ] |
| XRD, FTIR, XPS | 2019 | Graphene oxide, nano alumina | [ ] |
| XRD, XRF, SEM, PSA | 2018 | SiO , Na SiO | [ ] |
| XRD, RIR, MIF, Rietveld, Full Pattern Summation | 2018 | Clay minerals | [ ] |
| XRD, NMR, GNMD | 2018 | Clay minerals, hectorite | [ ] |
| In-situ XRD, Isothermal Calorimetry | 2018 | Fly ash, metakaolin, slag | [ ] |
| XRD, XRF | 2018 | Clay minerals, mica, mudrock | [ ] |
| XRD, ICP-OES, HRTEM | 2017 | Clay minerals, bioapatite | [ ] |
| XRD, conventional sintering, cold sintering | 2017 | Sillimanite | [ ] |
| MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
Share and Cite
Ali, A.; Chiang, Y.W.; Santos, R.M. X-ray Diffraction Techniques for Mineral Characterization: A Review for Engineers of the Fundamentals, Applications, and Research Directions. Minerals 2022 , 12 , 205. https://doi.org/10.3390/min12020205
Ali A, Chiang YW, Santos RM. X-ray Diffraction Techniques for Mineral Characterization: A Review for Engineers of the Fundamentals, Applications, and Research Directions. Minerals . 2022; 12(2):205. https://doi.org/10.3390/min12020205
Ali, Asif, Yi Wai Chiang, and Rafael M. Santos. 2022. "X-ray Diffraction Techniques for Mineral Characterization: A Review for Engineers of the Fundamentals, Applications, and Research Directions" Minerals 12, no. 2: 205. https://doi.org/10.3390/min12020205
Article Metrics
Article access statistics, further information, mdpi initiatives, follow mdpi.

Subscribe to receive issue release notifications and newsletters from MDPI journals
Help | Advanced Search
Condensed Matter > Materials Science
Title: deepxrd, a deep learning model for predicting of xrd spectrum from materials composition.
Abstract: One of the long-standing problems in materials science is how to predict a material's structure and then its properties given only its composition. Experimental characterization of crystal structures has been widely used for structure determination, which is however too expensive for high-throughput screening. At the same time, directly predicting crystal structures from compositions remains a challenging unsolved problem. Herein we propose a deep learning algorithm for predicting the XRD spectrum given only the composition of a material, which can then be used to infer key structural features for downstream structural analysis such as crystal system or space group classification or crystal lattice parameter determination or materials property predictions. Benchmark studies on two datasets show that our DeepXRD algorithm can achieve good performance for XRD prediction as evaluated over our test sets. It can thus be used in high-throughput screening in the huge materials composition space for new materials discovery.
| Comments: | 17 pages |
| Subjects: | Materials Science (cond-mat.mtrl-sci) |
| Cite as: | [cond-mat.mtrl-sci] |
| (or [cond-mat.mtrl-sci] for this version) | |
| Focus to learn more arXiv-issued DOI via DataCite |
Submission history
Access paper:.
- Other Formats
References & Citations
- Google Scholar
- Semantic Scholar
BibTeX formatted citation
Bibliographic and Citation Tools
Code, data and media associated with this article, recommenders and search tools.
- Institution
arXivLabs: experimental projects with community collaborators
arXivLabs is a framework that allows collaborators to develop and share new arXiv features directly on our website.
Both individuals and organizations that work with arXivLabs have embraced and accepted our values of openness, community, excellence, and user data privacy. arXiv is committed to these values and only works with partners that adhere to them.
Have an idea for a project that will add value for arXiv's community? Learn more about arXivLabs .
An official website of the United States government
The .gov means it’s official. Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.
The site is secure. The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.
- Publications
- Account settings
- My Bibliography
- Collections
- Citation manager
Save citation to file
Email citation, add to collections.
- Create a new collection
- Add to an existing collection
Add to My Bibliography
Your saved search, create a file for external citation management software, your rss feed.
- Search in PubMed
- Search in NLM Catalog
- Add to Search
X-ray diffraction: instrumentation and applications
Affiliation.
- 1 a SCIENT by CROMATEC_PLUS SRL, Research Center for Instrumental Analysis , Bucharest , Romania.
- PMID: 25831472
- DOI: 10.1080/10408347.2014.949616
X-ray diffraction (XRD) is a powerful nondestructive technique for characterizing crystalline materials. It provides information on structures, phases, preferred crystal orientations (texture), and other structural parameters, such as average grain size, crystallinity, strain, and crystal defects. X-ray diffraction peaks are produced by constructive interference of a monochromatic beam of X-rays scattered at specific angles from each set of lattice planes in a sample. The peak intensities are determined by the distribution of atoms within the lattice. Consequently, the X-ray diffraction pattern is the fingerprint of periodic atomic arrangements in a given material. This review summarizes the scientific trends associated with the rapid development of the technique of X-ray diffraction over the past five years pertaining to the fields of pharmaceuticals, forensic science, geological applications, microelectronics, and glass manufacturing, as well as in corrosion analysis.
Keywords: X-ray diffraction; applications; theory.
PubMed Disclaimer
Similar articles
- Applications of Powder X-Ray Diffraction in Small Molecule Pharmaceuticals: Achievements and Aspirations. Thakral NK, Zanon RL, Kelly RC, Thakral S. Thakral NK, et al. J Pharm Sci. 2018 Dec;107(12):2969-2982. doi: 10.1016/j.xphs.2018.08.010. Epub 2018 Aug 23. J Pharm Sci. 2018. PMID: 30145209 Review.
- Quantitative analysis of crystalline pharmaceuticals in tablets by pattern-fitting procedure using X-ray diffraction pattern. Takehira R, Momose Y, Yamamura S. Takehira R, et al. Int J Pharm. 2010 Oct 15;398(1-2):33-8. doi: 10.1016/j.ijpharm.2010.07.043. Epub 2010 Jul 30. Int J Pharm. 2010. PMID: 20674727
- Strain measurement of pure titanium covered with soft tissue using X-ray diffraction. Fujisaki K, Tadano S. Fujisaki K, et al. J Biomech Eng. 2010 Mar;132(3):031004. doi: 10.1115/1.4000935. J Biomech Eng. 2010. PMID: 20459192
- Observation of divergent-beam X-ray diffraction from a crystal of diamond using synchrotron radiation. Glazer AM, Collins SP, Zekria D, Liu J, Golshan M. Glazer AM, et al. J Synchrotron Radiat. 2004 Mar 1;11(Pt 2):187-9. doi: 10.1107/S0909049504000949. Epub 2004 Feb 12. J Synchrotron Radiat. 2004. PMID: 14960784
- Phase recovery and lensless imaging by iterative methods in optical, X-ray and electron diffraction. Spence JC, Weierstall U, Howells M. Spence JC, et al. Philos Trans A Math Phys Eng Sci. 2002 May 15;360(1794):875-95. doi: 10.1098/rsta.2001.0972. Philos Trans A Math Phys Eng Sci. 2002. PMID: 12804284 Review.
- Synthesis, Structural, and Optical Properties of 2-(2-methyl 8-hydroxyquinoline) Magnesium Nanorods for Optical Display Systems. Suchitra JP, Rhoda JC, Bharathi Devi V, Divya P, Albert HM. Suchitra JP, et al. J Fluoresc. 2024 Apr 16. doi: 10.1007/s10895-024-03724-7. Online ahead of print. J Fluoresc. 2024. PMID: 38625575
- The Impact of Vegetable Fibres on the Shrinkage and Mechanical Properties of Cob Materials. Kabore A, Ouellet-Plamondon CM. Kabore A, et al. Materials (Basel). 2024 Feb 3;17(3):736. doi: 10.3390/ma17030736. Materials (Basel). 2024. PMID: 38591571 Free PMC article.
- Mesoporous Ag@WO 3 core-shell, an investigation at different concentrated environment employing laser ablation in liquid. Salim ET, Saimon JA, Muhsin MS, Fakhri MA, Amin MH, Azzahrani AS, Ibrahim RK. Salim ET, et al. Sci Rep. 2024 Mar 5;14(1):5473. doi: 10.1038/s41598-024-55146-x. Sci Rep. 2024. PMID: 38443371 Free PMC article.
- Modular, multi-robot integration of laboratories: an autonomous workflow for solid-state chemistry. Lunt AM, Fakhruldeen H, Pizzuto G, Longley L, White A, Rankin N, Clowes R, Alston B, Gigli L, Day GM, Cooper AI, Chong SY. Lunt AM, et al. Chem Sci. 2023 Dec 26;15(7):2456-2463. doi: 10.1039/d3sc06206f. eCollection 2024 Feb 14. Chem Sci. 2023. PMID: 38362408 Free PMC article.
- Synthesis and characterizations of conocarpus- and azadirachta-derived activated carbons as wastewater recycling material. Mehdi M, Baig MH, Ahmad M, Ali K, Mohib M, Farooqi A, Affan M, Mazin M. Mehdi M, et al. Environ Monit Assess. 2024 Feb 13;196(3):262. doi: 10.1007/s10661-024-12423-6. Environ Monit Assess. 2024. PMID: 38351411
Publication types
- Search in MeSH
LinkOut - more resources
Full text sources.
- Taylor & Francis
Other Literature Sources
- The Lens - Patent Citations
Miscellaneous
- NCI CPTAC Assay Portal
- Citation Manager
NCBI Literature Resources
MeSH PMC Bookshelf Disclaimer
The PubMed wordmark and PubMed logo are registered trademarks of the U.S. Department of Health and Human Services (HHS). Unauthorized use of these marks is strictly prohibited.
Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.
- View all journals
- Explore content
- About the journal
- Publish with us
- Sign up for alerts
- Open access
- Published: 17 May 2019
Fast and interpretable classification of small X-ray diffraction datasets using data augmentation and deep neural networks
- Felipe Oviedo ORCID: orcid.org/0000-0001-9480-6539 1 na1 ,
- Zekun Ren 2 na1 ,
- Shijing Sun 1 ,
- Charles Settens 1 ,
- Zhe Liu 1 ,
- Noor Titan Putri Hartono ORCID: orcid.org/0000-0002-0748-0620 1 ,
- Savitha Ramasamy 3 ,
- Brian L. DeCost 4 ,
- Siyu I. P. Tian ORCID: orcid.org/0000-0002-8709-1798 1 ,
- Giuseppe Romano 1 ,
- Aaron Gilad Kusne 4 &
- Tonio Buonassisi 1 , 2
npj Computational Materials volume 5 , Article number: 60 ( 2019 ) Cite this article
24k Accesses
18 Altmetric
Metrics details
- Characterization and analytical techniques
- Computational methods
- Synthesis and processing
X-ray diffraction (XRD) data acquisition and analysis is among the most time-consuming steps in the development cycle of novel thin-film materials. We propose a machine learning-enabled approach to predict crystallographic dimensionality and space group from a limited number of thin-film XRD patterns. We overcome the scarce data problem intrinsic to novel materials development by coupling a supervised machine learning approach with a model-agnostic, physics-informed data augmentation strategy using simulated data from the Inorganic Crystal Structure Database (ICSD) and experimental data. As a test case, 115 thin-film metal-halides spanning three dimensionalities and seven space groups are synthesized and classified. After testing various algorithms, we develop and implement an all convolutional neural network, with cross-validated accuracies for dimensionality and space group classification of 93 and 89%, respectively. We propose average class activation maps, computed from a global average pooling layer, to allow high model interpretability by human experimentalists, elucidating the root causes of misclassification. Finally, we systematically evaluate the maximum XRD pattern step size (data acquisition rate) before loss of predictive accuracy occurs, and determine it to be 0.16° 2 θ , which enables an XRD pattern to be obtained and classified in 5.5 min or less.
Similar content being viewed by others
Automated classification of big X-ray diffraction data using deep learning models

Identification of crystal symmetry from noisy diffraction patterns by a shape analysis and deep learning
Automatic identification of crystal structures and interfaces via artificial-intelligence-based electron microscopy
Introduction.
High-throughput material synthesis and rapid characterization are necessary ingredients for inverse design and accelerated material discovery. 1 , 2 X-ray diffraction (XRD) is a workhorse technique to determine crystallography and phase information, including lattice parameters, crystal symmetry, phase composition, density, space group, and dimensionality. 3 This is achieved by comparing XRD patterns of candidate materials with the measured or simulated XRD patterns of known materials. 4 Despite its indispensable utility, XRD is a common bottleneck in materials characterization and screening loops: 1 hour is typically required for XRD data acquisition with high angular resolution, and another 1–2 hours are typically required for Rietveld refinement by an expert crystallographer, assuming the possible crystalline phases are known. It is widely recognized that machine learning methods have potential to accelerate this process; however, practical implementations have thus far focused on well-established materials, 5 , 6 , 7 require combinatorial datasets spanning among various phases, 8 , 9 or require large datasets, 5 , 10 whereas material screening using the inverse design paradigm often involves less-studied materials, spanning multiple classes of different material/phase compositions, and smaller prototype datasets.
Typically, experimental XRD pattern data are analyzed by obtaining descriptors such as peak shape, height, and position. Matching descriptors of the test pattern to known XRD patterns in crystalline databases allows the identification of the compound of interest. 4 Refinement methods such as Rietveld refinement and Pawley refinement have been used for decades to analyze experimental XRD patterns. 4 For novel compounds in thin-film form, however, the use of Rietveld refinement is limited due to the lack of reference patterns in material databases, as well as unknown film textures. The direct-space method, statistical methods, and the growth of single crystals have been used to obtain crystal symmetry information for novel materials, 7 , 11 , 12 , 13 , 14 but the significant iteration time, feature engineering, human expertise, and knowledge of specific material required makes these methods impractical for high-throughput experimentation, where sample characterization rates are of the order of one material per minute or faster, 2 , 15 explored over various material families.
An alternative approach consists in using machine learning methods to obtain more robust spectral descriptors and quickly classify crystalline structure based on peak location and shape in the XRD pattern. Breakthrough methods have been developed for the similar problem of phase attribution in combinatorial alloys, 16 , 17 but only few studies have been developed for solution-processed material screening, such as perovskite screening, where phase attribution is usually not as important as correct classification of materials into groups according to crystal parameters. The most successful methods 10 , 18 for material screening use convolutional neural networks (CNNs) trained with hundreds of thousands of XRD powder patterns simulated with data from the Inorganic Crystalline Structure Database (ICSD). Further CNN and other deep learning algorithms have been employed to obtain crystalline information for other kinds of diffraction data. 19 , 20 , 21 In a couple studies, noise-based data augmentation, a common technique of image preprocessing for machine learning, has been used to avoid overfitting in a broader kind of X-ray characterization problems 20 , 22 , 23 and more broadly in other fields such as Tramission Electron Microscopy imaging; 21 however, the augmentation procedure has not been based in physical knowledge of actual experimental samples. Furthermore, the best-performing machine learning methods developed up-to-date for XRD analysis do not allow any kind of interpretation by the experimentalists, 10 hindering improvements of experimental design.
While similar approaches produce good results for crystal structure classification, we have found that applying them to high-throughput characterization of novel solution-processed compounds is generally not practical, given the limited access to large datasets of clean, preprocessed, relevant, XRD spectra. Furthermore, most materials of interest developed in high-throughput synthesis loops are thin-film materials. The preferred orientation of the crystalline planes in thin-films causes their experimental XRD patterns to differ from the thousands of simulated XRD powder patterns available in most databases. 24 , 25 Thin-film compounds usually will present spectrum shifting and periodic scaling of peaks in preferred orientations, reducing the accuracy of machine learning models trained with powder data, 8 , 9 , 26 even in the cases when noise-based data augmentation techniques are used. 18
Considering these challenges, we propose a supervised machine learning framework for rapid crystal structure identification of novel materials from thin-film XRD measurements. For this work, we created a library of 164 XRD patterns of thin-film halide materials extracted from the >100,000 compounds available in the ICSD 27 ; these 164 XRD patterns include lead halide perovskite 28 , 29 and lead-free perovskites-inspired materials. 30 These XRD patterns were manually classified among different crystal dimensionalities using ICSD information. Based on this small dataset of relevant XRD powder patterns extracted from the ICSD and an additional 115 experimental XRD patterns, we propose a model-agnostic, physics-informed data augmentation to generate a suitable and robust training dataset for thin-film materials, and subsequently test the space group and dimensionality classification accuracy of multiple machine learning algorithms. A one-dimensional (1D) implementation of an “ all convolutional neural network ” (a-CNN) 31 is proposed, implemented and identified as the most accurate and interpretable classifier for this problem. We propose a new way to use class activation maps (CAMs), 32 computed from the weight distribution of a global average pooling layer and adapted to the context of our problem, to provide interpretability of root causes of classification success or failure to the experimentalist. Subsequently, the effect of the augmented dataset size and the XRD pattern granularity is investigated. Our proposed methodology could be applied to other crystal descriptors of thin-film materials, such as lattice parameters or atomic coordinates, as long as labeled information is available.
Our contributions can be summarized as: (a) development of physics-informed data augmentation for thin-film XRD, which successfully addresses the sparse/scarce data problem, breaching the gap between the thousands of XRD patterns in crystalline databases and real thin-film materials, (b) development of highly interpretable, highly accurate, a-CNN for XRD material screening, (c) proposal of average class activation maps as a feasible interpretability tool in CNNs trained on spectral data.
Results and discussion
Framework for rapid xrd classification.
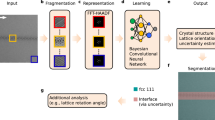
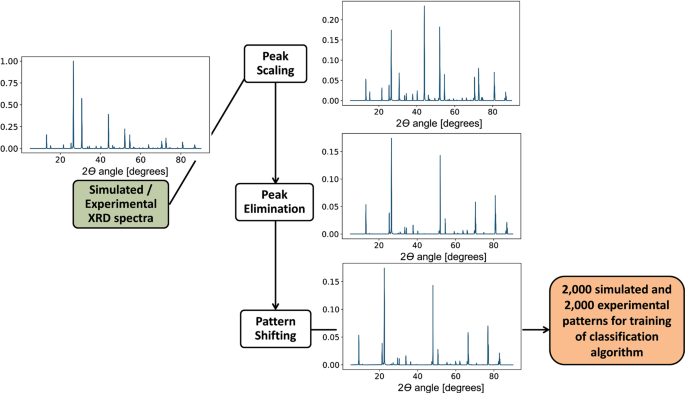
The framework developed for rapid classification of XRD thin-film patterns according to crystal descriptors is shown in Fig. 1a . The methodology makes use of both experimental and simulated XRD patterns to train a machine learning classification algorithm. A simulated dataset is defined by extracting crystal structure information from the ICSD. The experimental dataset consists of a set of synthesized samples, which are manually labeled for training and testing purposes. The datasets are subjected to data augmentation based on the three spectral transformations shown in Fig. 2 .
General framework and a-CNN architecture. a Schematic of our X-ray diffraction data classification framework, with physics-informed data augmentation. b Schematic of the best-performing algorithm, our all convolutional neural network
Physics-informed data augmentation: schematic of the physics-informed data augmentation algorithm, which accounts for the particularities of thin-film XRD spectra, as described by the subsequent transformations stated in Eqs. 1 – 3
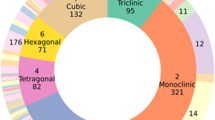
The crystal descriptors of interest, space group and crystal dimensionality , are chosen because of their importance for material screening in accelerated material development. In many inorganic material systems, the crystalline dimensionality—i.e., a generalization of the crystalline symmetry into 0-dimensional (0D), 1D, 2D, or 3D symmetry— constitutes a figure of merit for experimental material screening as it correlates with observed charge-transport properties. 33 In perovskites and perovskites-inspired materials, for instance, 3D crystalline structures have been shown to have good carrier-transport properties for solar cells and light-emitting diode applications, 33 , 34 whereas 3D–2D mixtures have been found to have greater stability in lead halide perovskites than pure-phase 3D crystals. 35 With further detail, the space group number describes the standardized symmetry group of a configuration in space, classifying crystal symmetries into 230 groups. Identifying the space group number of a sample provides crystal information beyond dimensionality, including atomic bonding angles and relative distances, which are believed to be of importance for predicting material properties. 36 In this specific study, the framework relies on the relation between XRD patterns and the crystal descriptors of interest. For example, among perovskite-inspired materials for photovoltaic applications, 3D cubic lead halide perovskites of multiple compositions show distinct features in their XRD patterns compared with 2D layered bismuth perovskites. 37 , 38
Typically, the powder XRD pattern is used to identify space group through Rietveld refinement, but the compression of crystalline 3D crystallographic information into a 1D diffraction pattern causes the space group to be impossible to determine unambiguously in certain low-symmetry phases, independently of the measurement technique. 39 In this work, the space groups of interest are able to be determined from XRD information only.
To better account for noise measurement and the physical difference between randomly oriented powder patterns and experimental thin-film patterns, the patterns were subjected to a process of data augmentation based on domain knowledge. Subsequently, both augmented experimental and simulated XRD pattern datasets are used for testing, training and cross-validation of machine learning algorithms.
Figure 1b shows the architecture of the final a-CNN, which is proposed and identified as the best-performing machine learning algorithm in subsequent sections.
Experimental measurement and labeling of XRD patterns
The experimental dataset consists of 75 XRD patterns for dimensionality classification, summarized in Supplementary Table S1 , and 88 XRD patterns for space group classification, summarized in Supplementary Table S2 . A total of 115 unique labeled XRD patterns are considered among both datasets. For this work, perovskites-inspired 3D materials based on lead halide perovskites (space group \(Pm\bar 3m\) ), tin halide perovskite ( I 4/ mcm ), cesium silver bismuth bromide double perovskite ( \(Fm\bar 3m\) ), bismuth and antimony halide 2D ( \(P\bar 3m1\) , \({\it Pc}\) , \({P2}_{1}{\!/\!a}\) ), and 0D ( P 6 3 / mmc ) perovskite-inspired materials are synthesized and used as training and testing dataset. The details of the synthesis and characterization methodology are described in great detail in our experimental study. 40 Supplementary Fig. S1 shows the t-Distributed Stochastic Neighbor Embedding representation of the XRD patterns labeled with dimensionality and space group, providing evidence of the complexity of the classification problem.
In this case, Rietveld refinement is restricted due to the unknown preferred orientation and texture of the thin-film samples. In consequence, the XRD patterns are subjected to peak indexing and the dimensionality and space group are labeled based on ICSD data.
Data mining and simulation of XRD patterns
The simulated training dataset consists of 164 compounds extracted from ICSD with a similar composition, expected crystal symmetry, and space group as the synthesized materials of interest. All the possible single, double, ternary, and quaternary combinations of the elements of interest were extracted during database mining. The compositions of all the materials of interest along with labeled dimensionality and space group information is available in Supplementary Table S3 . The fundamental crystal descriptors extracted from the material database are used to simulate XRD powder patterns with random crystalline orientations, as explained in the Methods section.
Data augmentation based on domain knowledge
Experimental thin-film XRD patterns vary greatly compared to simulated, idealized, randomly oriented XRD patterns. Due to expansions and contractions in the crystalline lattice, XRD peaks shift along the 2 ϴ axis according to the specific size and location of the different elements present in a compound, while maintaining similar periodicity based on crystal space group. 3 , 8 , 26 , 41 In addition, for thin-film samples, the XRD pattern can be shifted due to strain in the film induced during the fabrication process. 42 Polycrystalline thin-films are also known to have preferred orientations along certain crystallographic planes. The preferred orientation is influenced by the crystal growth process and the growth substrate, 24 and is common for most solution-processing and vapor-deposition fabrication methods. Ideal random powders contain multiple grains without any preferred global orientations, thus all crystallographic orientations are represented evenly in the peak intensity and periodicity of the XRD pattern. As a consequence of their preferred orientations along crystallographic planes, thin-film XRD relative peak intensities are scaled up periodically in the preferred plane orientation, and scaled down periodically or even eliminated in the non-preferred orientations.
To increase the size and robustness of the limited training dataset and to account for these fundamental differences between real thin-films and simulated XRD powder patterns, we perform a three-step data augmentation procedure based on physical domain knowledge:
( 1 ) Peak scaling, ( 2 ) Peak elimination, and ( 3 ) Pattern shifting. These transformation are described in detail in Methods. Figure 2 summarizes the data augmentation steps and its effects on a representative pattern. Given the hyperparameters S and ε in Eqs. 1 – 3 in the Methods section, 2000 patterns are augmented from the simulated dataset, and 2000 patterns are augmented from experimentally measured spectra.
We choose to perform physics-informed data augmentation instead of explicit regularization for the following reasons: ( 1 ) data augmentation has been found to be more robust at avoiding overfitting than explicit regularization when using convolutional neural networks, 43 ( 2 ) data augmentation is model-agnostic, allowing our approach to successfully bridge the gap between experimental XRD patterns and thousands of XRD patterns available in databases without depending on a specific model that might not generalize well in all cases ( no-free-lunch theorem ), and ( 3 ) physics-informed data augmentation allows high interpretability, and is found to be more robust than traditional noise-based data augmentation approaches (Supplementary Table S6 ).
Classification results and a-CNN
Preprocessed, augmented experimental data, and augmented simulated data are fed into various supervised machine learning algorithms for training and testing purposes. The best-performing algorithm is evaluated. The XRD patterns are classified into three crystal dimensionalities (0D, 2D, and 3D) and seven space groups ( \(Pm\bar 3m\) , I 4/ mcm , \(Fm\bar 3m,P\bar 3m1\) , \({Pc}\) , P 2 1 / a , and P 6 3 / mmc ).
For this purpose, we represent the XRD pattern as either a vector or a time series. For each kind of data representation, different classification algorithms are considered. Using a vector representation of the XRD pattern, the following classification methods are tested: Naive Bayes, k -Nearest Neighbors, Logistic Regression, Random Forest, Decision Trees, Support Vector Machine, Gradient Boosting Decision Trees, a Fully Connected Deep Neural Network, and an a-CNN with a global pooling layer. 44 , 45 , 46 The XRD patterns are also analyzed as a time series with a normalized Dynamic Time Warping (DTW) distance metric 47 combined with a k -Nearest Neighbors classification algorithm, which was found in literature as the most adequate metric for measuring similarity among metal-alloy XRD spectra. 7 , 26
The problem of novel material development is inherently a multi-class classification problem, in which the classes for training and testing purposes can often be imbalanced as some material families are better characterized than others (e.g., lead-based perovskites are better represented in material databases than newer lead-free perovskites). 38 Common metrics for binary classification such as accuracy might not be the most adequate in this context. 45 The final choice for adequate metrics depends on the relative importance of false positive and false negatives in minority and majority classes, according to the goals of the experimentalist. For method development in this work, we consider the following metrics: subset accuracy , defined as the number of correctly classified patterns among all test patterns, and F 1 score. F 1 score in this problem can be interpreted as the weighted harmonic mean of precision and recall; the closer it is to 1.0, the higher the classifier’s precision and recall. 45 Intuitively, precision is the ability of the classifier not to produce a false positive, whereas recall is the ability of a classifier to find all the true positives. An F 1 metric is calculated for each class label, and it is combined into an overall score by taking either the micro or the macro average of the individual scores. The macro average calculates the mean of the metrics of all the individual classes, hence treating all classes equally. The micro average adds the individual contribution of all samples to compute the overall metric.
When there is class imbalance, accuracy and F 1 micro score characterize the classifier’s performance over all classes, whereas F 1 macro emphasizes the accuracy on infrequent classes. 45 Thus, a natural choice for high-throughput experiments across multiple material classes seems to be accuracy/F 1 micro score, except in those cases when we are especially interested in analyzing an infrequent material class, being F 1 macro a more representative metric in that case. In this work, we choose to report the classification accuracy and both F 1 micro and F 1 macro , whereas recall and precision results are included in the Supplementary Information (Supplementary Tables S4 and S5 ).
We measure the performance of the dimensionality and space group classification methods based on three different approaches of splitting the training and testing datasets:
Case 1: Exclusively simulated XRD patterns are used for testing and training. Fivefold cross-validation is performed.
Case 2: The simulated XRD patterns are used for training, and the experimental patterns for known materials are used for testing.
Case 3: All of the simulated data and 80% of the experimental data are used for training, and 20% of the experimental data are used for testing. Fivefold cross-validation is performed.
Each one of the training/testing cases mentioned earlier are tested for crystal dimensionality and space group prediction accuracy and micro / macro F 1 score. The results are reported in Table 1 . In each cell, the crystal dimensionality classification metric is reported first, followed by the metric for space group classification. Case 1, presenting fivefold cross-validation results of the simulated dataset, has the highest accuracy as it does not predict any experimental data and thus is free of experimental errors for both crystal descriptors. Case 2 performs the experimental prediction solely based on simulated patterns, thus having the lowest accuracy. Finally, Case 3 has a significant higher accuracy than Case 2 for both crystal dimensionality and space group prediction. F 1 scores follow these trends as well.
In general, the model’s accuracy and F 1 score is lower for space group classification than that for crystal dimensionality classification. This discrepancy is caused by the lower number of per-class labeled examples for space group classification compared to crystal dimensionality classes. Class imbalance can also systematically affect the training performance of the classifier, to avoid this issue, we performed an oversampling test with synthetic training data according to, 48 , 49 and observed little discrepancy of accuracy between the balanced and imbalanced datasets after fivefold cross-validation.
The use of experimental data as part of the training set increases the model’s accuracy and robustness. This fact can be explained by the high variability of experimental thin-film XRD patterns, even after data preprocessing. The relatively high accuracy with the relatively small number of experimental samples (on the order of 10–10 2 ) confirms the potential of our data augmentation strategy to yield high predictive accuracies even with small datasets. Supplementary Table S6 in the Supplementary Information compares our strategy with traditional noise-based augmentation approaches, and shows an average increase of classification accuracy of >12% absolute.
Naturally, the F 1 macro score is systematically lower than the F 1 micro score, reflecting the impact of misclassification of those dimensionality and space group classes with less training examples. However, the F 1 macro score is still fairly high for most classifiers. This fact reflects the importance of adequate experimental design to achieve good generalization among classes.
For all three test cases, the a-CNN classifier performs better than any other classification technique. The 1D a-CNN architecture implemented is composed of three 1D convolutional layers, with 32 filters each, and strides and kernel sizes of 8, 5, and 3 units, respectively. The activation function between layers is ReLu . A global average pooling layer 50 (acting as a weak regularizer) and a final dense layer with softmax activation is used. The loss function minimized is binary cross entropy. We use early stopping with a batch size of 128 during training, and use the Adam optimizer algorithm to minimize the loss function. The CNN is implemented in Keras 2.2.1 with the Tensorflow background. Figure 1b contains a schematic of the proposed a-CNN architecture.
Our a-CNN architecture, in contrast with other CNNs, does not have max pooling layers between convolutional layers, and also lacks a set of dense layers in the final softmax classification layer. These modifications, in contrast with the architectures used in, 10 , 18 significantly reduces the number of parameters in the neural network, allows faster and simpler training, and are less prone to overfitting. Another advantage of our implementation is the possibility to extract CAMs from the weight distribution of the global average pooling layer. This characteristic of the network, properly adapted to our problem, allows us to visualize how the classified XRD patterns are mapped to the weight distribution at the end of the a-CNN. The results are further discussed in the interpretability subsection.
The a-CNN trained after data augmentation has an accuracy of >93 and 89% for crystal dimensionality and space group classifications, respectively. As far as we know, the accuracy is among the highest described in literature for space group classification algorithms, comparable to those trained with thousands of ICSD patterns and manual labeling by human experts, 10 , 51 and is also comparable to similar approaches in other kinds of diffraction data. 8 , 19 The neural network seems to be the most adequate method for high-throughput synthesis and characterization loops, as it also performs relatively well in terms of algorithm speed and in conditions of class imbalance. In the future, our methodology can be extended to other materials systems, and may include other crystal descriptors as predicted outputs, such as lattice parameters and atomic coordinates.
Furthermore, the a-CNN performs better than the traditional k -nearest neighbors method using DTW. In our test case and dataset, the differences between thin-film and powder spectra seem not to be captured properly by DTW alone. Arguably, DTW could be more useful if a larger XRD thin-film pattern dataset is available for k -Nearest Neighbors classification, or if it exists greater similarity between XRD patterns of the same class, allowing the DTW warping path to be better captured within the DTW window under consideration. 26 CNNs have been found to perform better than DTW for classification of time series, which is consistent with our results. 52
Effect of augmented dataset size
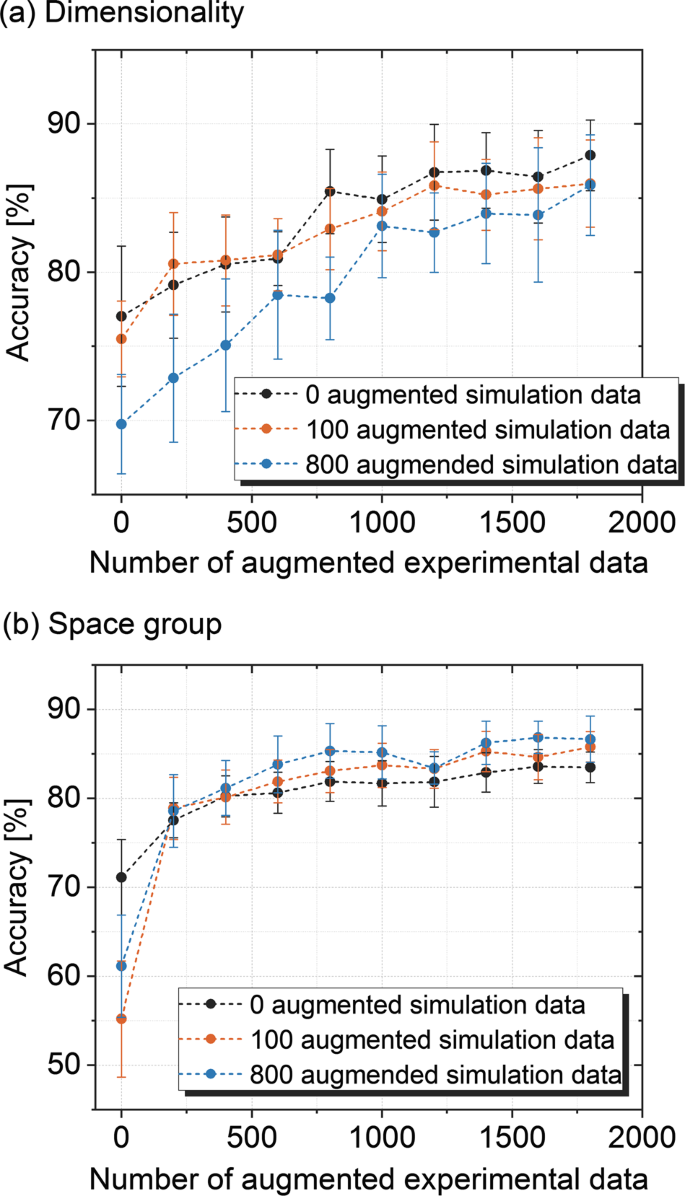
The size of the dataset is critical for obtaining a high accuracy and F 1 score. To explore the effect of augmented dataset size, the a-CNN accuracy was computed for various combinations of augmented experimental patterns (i.e., number of augmented XRD spectra originated from the 88 measured spectra, varying S and ε in Eqs. 1 – 3 ) and augmented simulated dataset sizes (i.e., number of augmented XRD spectra originating from the 164 simulated ICSD spectra). Figure 3 a, b summarizes this sensitivity analysis for Case 3 training/testing conditions for dimensionality and space group classification. Twenty different fivefold cross-validation runs were performed to calculate the 1-standard deviation error bars for each data point.
Accuracy of the a-CNN model with augmented data: line plot showing mean Case 3 a-CNN accuracy, as a function of the number of augmented patterns (Methods, Eqs. 1 – 3 ) included in the training set, for ( a ) dimensionality classification and ( b ) space group classification. The x axis shows augmented experimental data (based on the original experimental XRD patterns), and the legend shows simulated data (based on the 164 simulated powder diffraction patterns obtained from the ICSD). The error bars correspond to one standard deviation from the mean
In general, as the size of the experimental and augmented datasets increase, the mean accuracy quickly approaches the asymptotic accuracy reported in Table 1 . This trend reaffirms and quantifies the importance of data augmentation for the predictive accuracy of our model.
The critical augmented dataset size seems to be around 700 augmented spectra. The model’s accuracy is more sensitive to the augmented experimental dataset size, likely because most of the dataset variance comes from the experimental XRD patterns. The data augmentation of the simulated dataset causes the accuracy to grow monotonically in Fig. 3b ; however, this trend is not satisfied in the case of Fig. 3a , where no augmented simulated data seems on average to perform the best. We hypothesize that augmenting simulated data could actually introduce excessive noise to the model, hampering classification when the number of possible classes is small.
Figure 3 illustrates that if no data augmentation is used (i.e., the origin, 0, 0), the predictive accuracy could be below 50% for space group and below 70% for dimensionality. Our physics-informed data augmentation directly increase accuracy by up to 23% in the case of dimensionality and 19% in the case of space group classification. This result reinforces the need for data augmentation for sparse/scarce datasets, as is typical with early-stage material development.
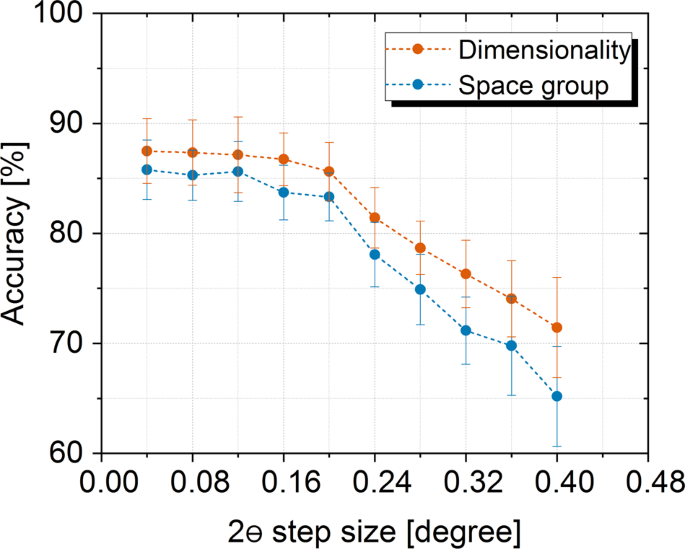
Impact of data coarsening
To evaluate the trade-offs between accuracy and XRD acquisition speed, we investigate how data coarsening of the XRD pattern impacts the accuracy of ML algorithm prediction. In Fig. 4 , we report Case 3 accuracy with increasing 2 ϴ angle step size. The baseline step size of the 2 ϴ scan in our XRD patterns is 0.04°. Data coarsening is performed by selectively removing the data with increasing step sizes and rerunning the augmentation and classification algorithms. For crystal dimensionality and space group classification, the highest accuracies are achieved at 0.04–0.08°, whereas 85%+ accuracy is achieved when the 2 ϴ step size is 0.16° or less for both cases. Using the larger step size, the XRD pattern acquisition time can be reduced by 75%, allowing the full spectra to be measured and classified in <5.5 min with our tool setup.
Reducing XRD pattern acquisition time: simulation of the trade-off between XRD pattern acquisition rate and predictive accuracy. Accuracies for crystal dimensionality and space group predictions are estimated by coarsening the XRD spectrum 2 ϴ step size for Case 3 conditions. The error bars correspond to one standard deviation from the mean
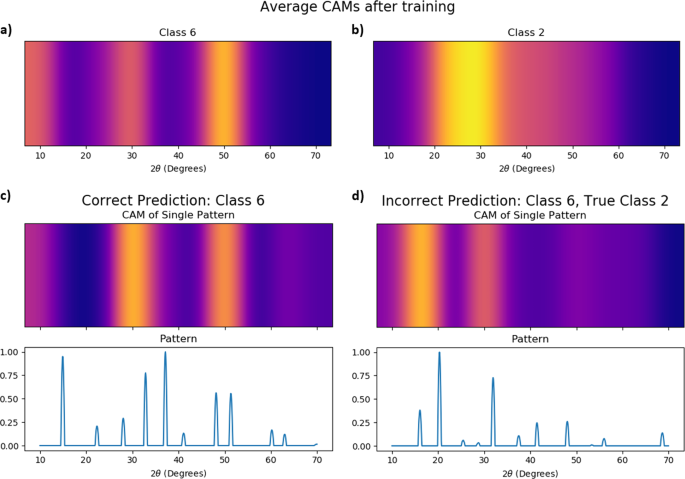
Interpretability using CAMs
Class activation maps (CAM) are representations of the weights in the last layer of a CNN, before performing classification. A CAM for a certain class and pattern indicates the main discriminative regions (in our case, peak and series of peaks in the XRD pattern) that the network uses to identify that class. 32 Details of the CAM computation are included in the Methods section.
A similar approach has been followed to interpret and improve object recognition in images and videos using 2D CNNs. 32 A single pattern or image produces a unique CAM revealing the main discriminative features. In addition, in the context of our problem, we propose to generalize CAMs to all training samples within a class by averaging over each of the computed CAM weights for all training samples within a class, as explained in the Methods section. This averaging procedure is justified as the location and periodicity of discriminative peaks within a class varies only slightly along all labeled samples in the training set, and can be extended to many spectral measurement techniques. This average CAM allows to visualize the main discriminative features of an XRD pattern that were used to classify all the training data belonging to a certain class.
By comparing the CAM for a single pattern with the average CAM for given class, we can identify the root causes of correct and incorrect classification by the a-CNN. Figure 5 illustrates this procedure for XRD patterns of space group classes Class 2 ( P 2 1 / a ) and Class 6 ( \(Pm\bar 3m\) ). Figure 5a, b shows the average CAM maps of Class 6 and Class 2 space groups. Figure 5c shows the CAM of an individual, correctly classified XRD pattern. If we compare the individual CAM with Class 6 Average CAM, we can see that the neural network is identifying the same reference pattern as most of Class 6 samples, which translates into classification as Class 6. In contrast, Fig. 5d shows an incorrectly classified XRD pattern, which was determined to belong to Class 6 by the CNN, when in reality it belongs to Class 2. A comparison of the individual CAM with the average CAMs of classes 6 and 2 reveals that the misclassified CAM is more similar to Fig. 5a than Fig. 5b . A closer look to the misclassified patterns, shows that the periodicity of peaks before 30° and the relative lack of peaks between 30° and 50° (likely caused by mixed phases), are causing the misclassification.
Class activation maps for misclassification interpretability: class activation maps (CAMs) generated by the a-CNN architecture, representing space group classification of Class 2 ( P 2 1 / a ) and Class 6 ( \(Pm\bar 3m\) ). ( a , b ) correspond to maps generated by averaging all training samples in a certain class, whereas ( c , d ) correspond to the CAMs of correctly classified and incorrectly classified individual patterns, respectively. The correctly predicted pattern of ( c ) is explained by the similarity of its CAM to the average CAM of Class 6; whereas, the incorrectly prediction ( d ) can be explained by comparing its CAM with the average CAMs of classes 2 and 6
Several representative misclassification cases are identified and included in the Section VII of Supplementary Information. In our work, by comparing the CAM of wrongly classified cases with the average CAM of all training data within certain class, we conclude there are three main causes for failed classification. The first cause is the mixture of phases in the sample, which increases the chance of the CAM of a particular pattern differing from the average class CAM. The second cause is lack of XRD patterns in the per-class training data. We only have <5 patterns in certain space group classes, thus the average CAM of minority classes has only a limited number of discriminative features compared to majority classes, increasing the testing error. The third cause of misclassification is missing peaks, or too few peaks, present in the XRD pattern; because of the lack of enough discriminative features, the CAM of the incorrectly labeled pattern could be ambiguously similar to two or more average class CAMs, causing the misclassification.
After the experimentalist identifies these root causes of error, they can be mitigated by increasing the number of experimental training points for certain classes or increasing the phase purity of the material coming from the synthesis and solution-processing procedure.
Summary of contributions
In this work, we develop a supervised machine learning framework to screen novel materials based on the analysis of their XRD spectra. The framework is designed specifically for cases when only sparse datasets are available, e.g., early-stage high-throughput material development and discovery loops. Specifically, we propose a physics-informed data augmentation method that extends small, targeted experimental and simulated datasets, and captures the possible differences between simulated XRD powder patterns and experimental thin-film XRD patterns. A few thousand augmented spectra are found to increase our classification accuracy from <60 to 93% for dimensionality and 89% for space group. The F 1 macro score is also over 0.85 for various algorithms, reflecting the model’s capacity to deal with significantly imbalanced classes.
When trained with both augmented simulated and experimental XRD spectra, a-CNNs are found to have the highest accuracy/ F 1 macro score among the many supervised machine learning methods studied. Our proposed a-CNN architecture allows high performance and interpretably through CAMs. The use of our proposed average CAMs, allow to identify the root cause of misclassification, and allow the design of a robust experiment. Furthermore, we find that the neural network model tolerates coarsening of the training data, providing future opportunities for online learning, i.e., the on-the-fly adaptive adjustment of XRD measurement parameters by taking feedback from machine learning algorithms. 15
Our approach can be extended to XRD-based high-throughput screening of any kind of thin-film materials, beyond perovskite and perovskite-inspired materials. Since most material databases lack information for various kinds of novel materials, the data augmentation approach to tackle data scarcity can be broadly applied. The underlying difference between XRD patterns of thin-films and powders is common to a broad range of materials and is commonly seen in most thin-film characterization experiments. The high interpretability of our approach could allow future work in semi-supervised or active learning, allowing the CAM maps to guide manual XRD refinement or actual XRD experiments. The framework may also be extended beyond XRD classification, to any spectrum containing information-rich features that require classification (XPS, XRF, PL, mass spectroscopy, etc.). The advantages of our approach include: ( 1 ) interpretable error analysis; ( 2 ) a data augmentation strategy that enables fast and accurate classification, even with small and imbalanced datasets.
Measurement and preprocessing of experimental XRD patterns
The XRD patterns for each sample are obtained by using a parallel beam, X-ray powder diffraction Rigaku SmartLab system 53 with 2ϴ angle from 5 to 60 ° with a step size of 0.04 ° . The tool is configured in a symmetric setup. We preprocess the raw XRD patterns to reduce the experimental noise and the background signal. For this purpose, the background signal is estimated and subtracted along the 2ϴ axis, and the spectrum is smoothed conserving the peak width and relative peak size applying the Savitzky-Golay filter. 54 A representative example of a preprocessed and raw XRD spectra is included in Supplementary Fig. S2 .
Simulation of powder XRD patterns
The powder XRD simulations are carried out with Panalytical Highscore v4.7 software based on the Rietveld algorithm implementation by Hill and Howard. 55 , 56 The XRD crystal is assumed to have fully random grain orientations. The unit cell lattice parameters, atomic coordinates, atomic displacement parameters, and space group information are considered for the structure factor calculation in the Rietveld model.
Physics-informed data augmentation
Suppose we describe the series of peaks in an XRD pattern by a discrete function \(\left( {2\theta } \right):I \to {\Bbb R}^ +\) , which maps a set of discrete angles I to positive real numbers \({\mathbb{R}^+}\) corresponding to peak intensities. We augment the data through the following sequential process of transformations \(\Phi _{S,c}^1,\Phi _S^2\) , and \(\Phi _\varepsilon ^3\) :
Random peak scaling is applied periodically along the 2 ϴ axis to account for different thin-film preferred orientations. A subset of random peaks at periodic angles S is scaled by factor c , such that
Random peak elimination (with a different randomly selected S than Eq. 1 ) is applied periodically along the 2 ϴ axis, to account for different thin-film preferred orientations, such that
Pattern shifting by small random value ε along the 2 ϴ direction to allow for different material compositions and film strain conditions, such that
We perform global average pooling in the last convolutional layer. The pooling results are defined as \(\mathop {\sum }\limits_x f_k\left( x \right)\) where f k ( x ) is the activation of unit k at convolution location x . The pooling results \(\mathop {\sum }\limits_x f_k\left( x \right)\) are subsequently fed into the softmax classifier. The class confidence score, thus can be computed as:
We define \(M_C\left( x \right) = \mathop {\sum}\nolimits_k {w_k^c} f_k\left( x \right)\) , as the CAM for class C , where \(w_k^C\) is the weight of unit k of the last convolution layer of class C. Therefore, Sc can be rewritten as:
M C ( x ) directly indicates the importance of the activation at the discrete location x for a given XRD pattern in class C .
In the context of XRD and other spectral measurements, the location of relevant intensity peaks is likely to be displaced only little from sample to sample within a certain class. Thus, the CAMs for all samples within a class are similar, and could be averaged to obtain the discriminative features during activation. Thus, we can define average CAMs for class C as \(\bar M_C\left( x \right)\) :
where n corresponds to the training patterns labeled as class C.
Data availability
The experimental dataset analyzed during the current study is available in the following GitHub repository: [ https://github.com/PV-Lab/AUTO-XRD/tree/master/Datasets/Experimental ]. The simulated and labeled data that support the findings of this study is available from the Inorganic Crystalline Structure Database (ICSD), but restrictions apply to the availability of these data, which were used under license for the current study, and so are not publicly available. Data are, however, available from the authors upon reasonable request and with permission of ICSD.
Code availability
The codes used for preprocessing, data augmentation, and classification are available in the GitHub repository [ https://github.com/PV-Lab/AUTO-XRD/ ]. The classification algorithms are implemented using scikit-learn 0.20 45 and the fastdtw python library. The a-CNN is implemented using Keras with the Tensorflow background.
Tabor, A., Roch, D. & Saikin, L. Lawrence Berkeley National Laboratory recent work title accelerating the discovery of materials for clean energy in the era of smart automation. Nat Rev Mater . https://doi.org/10.1038/s41578-018-0005-z (2018).
Article CAS Google Scholar
Correa-Baena, J.-P. et al. Accelerating materials development via automation, machine learning, and high-performance computing. Joule 2 , 1410–1420 (2018).
Dinnebier, R. E. Powder Diffraction: Theory and Practice . (RSC Publ, Cambridge, 2009).
Rietveld, H. M. A profile refinement method for nuclear and magnetic structures. J. Appl. Crystallogr. 2 , 65–71 (1969).
Carr, D. A., Lach-hab, M., Yang, S., Vaisman, I. I. & Blaisten-Barojas, E. Machine learning approach for structure-based zeolite classification. Microporous Mesoporous Mater. 117 , 339–349 (2009).
Baumes, L. A., Moliner, M., Nicoloyannis, N. & Corma, A. A reliable methodology for high throughput identification of a mixture of crystallographic phases from powder X-ray diffraction data. CrystEngComm 10 , 1321–1324 (2008).
Baumes, L. A., Moliner, M. & Corma, A. Design of a full-profile-matching solution for high-throughput analysis of multiphase samples through powder X-ray diffraction. Chem. - A Eur. J. 15 , 4258–4269 (2009).
Stanev, V. et al. Unsupervised phase mapping of X-ray diffraction data by nonnegative matrix factorization integrated with custom clustering. npj Comput. Mater . 4 , 43 (2018).
Kusne, A. G., Keller, D., Anderson, A., Zaban, A. & Takeuchi, I. High-throughput determination of structural phase diagram and constituent phases using GRENDEL. Nanotechnology 26 , 444002 (2015).
Park, W. B. et al. Classification of crystal structure using a convolutional neural network. IUCrJ . 4 , 486–494 (2017).
Park, W. B., Singh, S. P., Yoon, C. & Sohn, K. S. Combinatorial chemistry of oxynitride phosphors and discovery of a novel phosphor for use in light emitting diodes, Ca 1.5 Ba 0.5 Si 5 N 6 O 3 :Eu 2+ . J. Mater. Chem. C. 1 , 1832–1839 (2013).
Rybakov, V. B., Babaev, E. V., Pasichnichenko, K. Y. & Sonneveld, E. J. X-ray mapping in heterocyclic design: VI. X-ray diffraction study of 3-(isonicotinoyl)-2-oxooxazolo[3,2-a]pyridine and the product of its hydrolysis. Crystallogr. Rep. 47 , 473–477 (2002).
Google Scholar
Hirosaki, N., Takeda, T., Funahashi, S. & Xie, R. J. Discovery of new nitridosilicate phosphors for solid state lighting by the single-particle-diagnosis approach. Chem. Mater. 26 , 4280–4288 (2014).
Suram, S. K. et al. Automated phase mapping with AgileFD and its application to light absorber discovery in the V-Mn-Nb oxide system. ACS Comb. Sci. 19 , 37–46 (2017).
Ren, F. et al. Accelerated discovery of metallic glasses through iteration of machine learning and high-throughput experiments. Sci. Adv . 4 , eaaq1566 (2018).
Article Google Scholar
Bunn, J. K. et al. Generalized machine learning technique for automatic phase attribution in time variant high-throughput experimental studies. J. Mater. Res. 30 , 879–889 (2015).
Kusne, A. G. et al. On-the-fly machine-learning for high-throughput experiments: search for rare-earth-free permanent magnets. Sci. Rep. 4 , 1–7 (2014).
Vecsei, P. M. et al. Neural network-based classification of crystal symmetries from X-ray diffraction patterns. arXiv preprint arXiv:1812.05625 (2018).
Ziletti, A., Kumar, D., Scheffler, M. & Ghiringhelli, L. M. Insightful classification of crystal structures using deep learning. Nat. Commun. 9 , 1–10 (2018).
Ke, T. W. et al. A convolutional neural network-based screening tool for X-ray serial crystallography. J. Synchrotron Radiat. 25 , 655–670 (2018).
Ziatdinov, M. et al. Deep learning of atomically resolved scanning transmission electron microscopy images: chemical identification and tracking local transformations. ACS Nano. 11 , 12742–12752 (2017).
Le Bras, R. et al. A computational challenge problem in materials discovery: synthetic problem generator and real-world datasets. Proceedings of the Twenty-Eighth AAAI Conference of Artifical Intelligence System , pp. 438–443 (2014).
LeBras, R. et al. Constraint reasoning and kernel clustering for pattern decomposition with scaling. in Principles and Practice of Constraint Programming – CP 2011 (ed. Lee, J.) 508–522 (Springer, Berlin, Heidelberg, 2011).
Järvinen, M. Application of symmetrized harmonics expansion to correction of the preferred orientation effect. J. Appl. Crystallogr. 26 , 525–531 (1993).
Fewster, P. F., Langford, J. I. & Fewster, P. F. Reports on progress in physics related content X-ray analysis of thin films and multilayers. 59 , 11 (1996).
Iwasaki, Y., Kusne, A. G. & Takeuchi, I. Comparison of dissimilarity measures for cluster analysis of X-ray diffraction data from combinatorial libraries. npj Comput. Mater. 3 , 1–8 (2017).
Belkly, A., Helderman, M., Karen, V. L. & Ulkch, P. New developments in the Inorganic Crystal Structure Database (ICSD): accessibility in support of materials research and design. Acta Crystallogr. Sect. B Struct. Sci. 58 , 364–369 (2002).
Eperon, G. E. et al. Formamidinium lead trihalide: a broadly tunable perovskite for efficient planar heterojunction solar cells. Energy Environ. Sci. 7 , 982–988 (2014).
Lee, M. M., Teuscher, J., Miyasaka, T., Murakami, T. N. & Snaith, H. J. Efficient hybrid solar cells based on meso-superstructured organometal halide perovskites. Sci. (80-.) 338 , 643–647 (2012).
Hoye, R. L. Z. et al. Perovskite-inspired photovoltaic materials: toward best practices in materials characterization and calculations. Chem. Mater. 29 , 1964–1988 (2017).
Springenberg, J. T. et al. Striving for simplicity: the all convolutional net. arXiv preprint arXiv:1412.6806. (2014).
Zhou, B. et al. Learning deep features for discriminative localization. Proceedings of the IEEE conference on computer vision and pattern recognition . https://doi.org/10.1109/CVPR.2016.319 (2016).
Etgar, L. The merit of perovskite’s dimensionality; Can this replace the 3D halide perovskite? Energy Environ. Sci. 11 , 234–242 (2018).
Xiao, Z., Meng, W., Wang, J., Mitzi, D. B. & Yan, Y. Searching for promising new perovskite-based photovoltaic absorbers: the importance of electronic dimensionality. Mater. Horiz . https://doi.org/10.1039/C6MH00519E (2017).
Zhang, T., Long, M., Liu, P., Xie, W. & Xu, J.-B. Stable and efficient 3D-2D perovskite-perovskite planar heterojunction solar cell without organic hole transport layer. Joule https://doi.org/10.1016/j.joule.2018.09.022 (2018).
Kurchin, R. C., Gorai, P., Buonassisi, T. & Stevanović, V. Structural and chemical features giving rise to defect tolerance of binary semiconductors. Chem. Mater. 30 , 5583–5592 (2018).
Baikie, T. et al. Synthesis and crystal chemistry of the hybrid perovskite (CH3NH3)PbI3 for solid-state sensitised solar cell applications. J. Mater. Chem. A 1 , 5628–5641 (2013).
Sun, S. et al. Synthesis, crystal structure, and properties of a perovskite-related bismuth phase, (NH 4 ) 3 Bi 2 I 9 . APL Mater. 4 , 031101 (2016).
Coelho, A. A. TOPAS-Academic, Version 6: technical reference. (Coelho Software. Brisbane, Australia, 2016).
Shijing Sun, et al. Accelerating photovoltaic materials development via high-throughput experiments and machine-learning-assisted diagnosis. Joule 2 , 1410–1420 (2018).
Ermon, S. et al. Pattern decomposition with complex combinatorial constraints: application to materials discovery. AAAI'15 Proceedings of the Twenty-Ninth AAAI Conference on Artificial Intelligence . (2014).
Zhao, J. et al. Strained hybrid perovskite thin films and their impact on the intrinsic stability of perovskite solar cells. Sci. Adv. 3 , eaao5616 (2017).
Hernández-García, A. & König, P. Data augmentation instead of explicit regularization. arXiv preprint arXiv:1806.03852 (2018).
Goodfellow, I., Bengio, Y., Courville, A. & Bengio, Y. Deep Learning . 1 (MIT Press, Cambridge, 2016).
Pedregosa, F. et al. Scikit-learn: machine learning in {P}ython. J. Mach. Learn. Res. 12 , 2825–2830 (2011).
Friedman, J., Hastie, T. & Tibshirani, R. The Elements of Statistical Learning . 1 (Springer Series in Statistics, New York, NY, USA, 2001).
Salvador, S. & Chan, P. FastDTW: toward accurate dynamic time warping in linear time and space. Time 11 , 70–80 (2004).
Haixiang, G. et al. Learning from class-imbalanced data: review of methods and applications. Expert Syst. Appl. 73 , 220–239 (2017).
Chawla, N. V., Bowyer, K. W., Hall, L. O. & Kegelmeyer, W. P. SMOTE: synthetic minority over-sampling technique. J. Artif. Intell. Res. 16 , 321–357 (2002).
Lin, M., Chen, Q. & Yan, S. Network in network. arXiv preprint arXiv:1312.4400. (2013).
Yoon, C. H. et al. Unsupervised classification of single-particle X-ray diffraction snapshots by spectral clustering. Opt. Express 19 , 16542 (2011).
Wang, Z., Yan, W. & Oates, T. Time series classification from scratch with deep neural networks: a strong baseline. Proc. Int. Jt. Conf. Neural Netw. 2017 , 1578–1585 (2017).
Kobayashi, S. & Inaba, K. X-ray thin-film measurement techniques. Mass Spectrosc. Equipped a Ski. Interface 28 , 8 (2012).
CAS Google Scholar
Press, W. H. & Teukolsky, S. A. Savitzky-Golay smoothing filters. Comput. Phys. 4 , 669 (1990).
Hill, R. J. & Howard, C. J. Quantitative phase analysis from neutron powder diffraction data using the Rietveld method. J. Appl. Crystallogr. 20 , 467–474 (1987).
Degen, T., Sadki, M., Bron, E., König, U. & Nénert, G. The HighScore suite. Powder Diffr. 29 , S13–S18 (2014).
Download references
Acknowledgements
We thank FengXia Wei (A*STAR), Jason Hattrick-Simpers (NIST), Max Hutchinson (Citrine Informatics), and Zachary T. Trautt (NIST) for helpful suggestions on our analysis. Prof. Juan Pablo Correa Baena at Georgia Tech for sharing various experimental XRD patterns. This work was supported by a TOTAL SA research grant funded through MITei (supporting the experimental XRD), the National Research Foundation (NRF), Singapore through the Singapore Massachusetts Institute of Technology (MIT) Alliance for Research and Technology’s Low Energy Electronic Systems research program (supporting the machine learning algorithm development), the Accelerated Materials Development for Manufacturing Program at A*STAR via the AME Programmatic Fund by the Agency for Science, Technology and Research under Grant No. A1898b0043 (for ML algorithm error analysis), and by the U.S. Department of Energy under the Photovoltaic Research and Development program under Award DE-EE0007535 (for code framework development). This work made use of the CMSE at MIT, which is supported by NSF award DMR-0819762.
Author information
These authors contributed equally: Felipe Oviedo, Zekun Ren
Authors and Affiliations
Massachusetts Institute of Technology, Cambridge, MA, 02139, USA
Felipe Oviedo, Shijing Sun, Charles Settens, Zhe Liu, Noor Titan Putri Hartono, Siyu I. P. Tian, Giuseppe Romano & Tonio Buonassisi
Singapore-MIT Alliance for Research and Technology, Singapore, 138602, Singapore
Zekun Ren & Tonio Buonassisi
Institute for Infocomm Research (I2R), Agency for Science, Technology and Research (A*STAR), Singapore, 138632, Singapore
Savitha Ramasamy
National Institute of Standards and Technology, MS 8520, Gaithersburg, MD, 20899, USA
Brian L. DeCost & Aaron Gilad Kusne
You can also search for this author in PubMed Google Scholar
Contributions
F.O. and Z.R. contributed equally for this work. F.O., Z.R., S.S., and T.B. conceived of the research. C.S., F.O., and S.S. prepared the simulated XRD data. Z.R., F.O., C.S., B.L.D.C., and A.G.K. developed data augmentation. S.S., N.T.P.H., and C.S. collected the XRD data. F.O., Z.R., and G.R. developed and tested ML algorithms, with key intellectual contributions from R.S., Z.L., B.L.D.C., and A.G.K. F.O. and Z.R. implemented and tuned the final a-CNN architecture and adapted class activation maps to the context of the problem. F.O., Z.R., S.I.P.T., and T.B. wrote the manuscript, with input from all co-authors.
Corresponding authors
Correspondence to Felipe Oviedo , Zekun Ren or Tonio Buonassisi .
Ethics declarations
Competing interests.
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Supplementary information, rights and permissions.
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/ .
Reprints and permissions

About this article
Cite this article.
Oviedo, F., Ren, Z., Sun, S. et al. Fast and interpretable classification of small X-ray diffraction datasets using data augmentation and deep neural networks. npj Comput Mater 5 , 60 (2019). https://doi.org/10.1038/s41524-019-0196-x
Download citation
Received : 01 December 2018
Accepted : 25 April 2019
Published : 17 May 2019
DOI : https://doi.org/10.1038/s41524-019-0196-x
Share this article
Anyone you share the following link with will be able to read this content:
Sorry, a shareable link is not currently available for this article.
Provided by the Springer Nature SharedIt content-sharing initiative
Quick links
- Explore articles by subject
- Guide to authors
- Editorial policies
Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.
The Use of X-Ray Diffraction for Nanoparticle Characterization
- Download PDF Copy

X-ray diffraction (XRD) is a versatile technique used commonly in the field of nanotechnology to characterize and acquire accurate information regarding the composition, crystal structure, and crystalline grain size of nanoparticles.

Image Credit: Crevis/Shutterstock.com
XRD method is best suited for powdered samples, which are freshly prepared from drying the samples’ respective colloidal solutions. From the XRD equipment, the peaks’ position and intensity of a sample are compared with the patterns from various diffraction database references, which assists in quantifying the composition of nanoparticles (Mourdikoudis, Pallares, & Thanh, 2018).
The working principle of the XRD method involves the scattering of X-rays due to the revolution of electrons in the atom’s nucleus when the rays strike on the nanoparticles. The scattered X-rays are reflected in various directions, which cause interference patterns. These patterns are either destructive or constructive (Fultz & Howe, 2013) but only the scattered X-rays that undergo constructive interaction result in diffraction.
In a nanoparticle, constructive interference results when two waves are moving in phase with each other, and destructive interference results from out-of-phase movement. The atomic-scale arrangement and the diffraction are strongly and inversely correlated: atoms having shorter periodic arrangements show greater diffraction angles and vice versa (Fultz & Howe, 2013).
Characterization of Nanoparticles Using XRD
The characterization of the nanoparticles through XRD requires a source, a detector, and a sample.
Thin films of nanoparticles are prepared for XRD analysis, which involves drop-casting of the nanoparticle onto a suitable low-background substrate. Nanoparticle samples that have the orientation of interest are placed on a suitable goniometer, where several reflections are evaluated. However, a sample of random orientation may only require a quick scan through a 2θ diffraction angle.
Nanoparticles characterization from XRD begins with the identification of the sample material’s phase; the crystal type in the sample is determined through a search-match process, which is done in the regions where the peaks of high intensities are observed.
Related Stories
- Range of CCD Detection Systems for X-Ray Applications
- PDR’s New Affordable PCB X-ray Inspection Systems Offer Quality Image Clarity
- Microscopy Techniques for Art Conservation
Various XRD peak patterns are the results of various atom arrangements. In an XRD technique, the interference occurs when the light of a designated wavelength illuminates a periodic structure having a predefined spacing. The XRD principle follows Bragg’s law, (n*λ = 2*d*sinθ), where λ, n, d, and θ refers to X-ray wavelength, integer, atomic plane spacing, and diffraction half-angle, respectively. As a result, information regarding the sample’s crystal defects, crystal size, crystalline phase, shape anisotropy, strain, texture can be obtained from the evaluation of the diffraction peaks’ width, shape, and position (Widjonarko, 2016).
Importance of Nanoparticle Characterization
The characterization of nanoparticles has become increasingly important because they are synthesized from several mechanical or chemical routes (Koczkur, Mourdikoudis, Polavarapu, & Skrabalak, 2015), and they have huge potential technological applications and academic research interests across several fields.
Since nanoparticles have a large surface area-to-volume ratio, their properties are significantly altered with size, which makes the characterization an important step to understand their properties at different molecular levels.
Other properties, such as texture, strain, shape anisotropy, crystalline phase, crystal defects, and crystal size impact the chemical, electronic, mechanical, and optical attributes of the nanoparticles.
Without the proper characterization, the applicability of the specific nanoparticle would meet an immense challenge (Thanh, Maclean, & Mahiddine, 2014).
Key Research
In their research, (Wu, et al ., 2015) focused on investigating the eco-friendly gold nanoparticles and used XRD to confirm the single crystallinity nature of APM-AuNPs, demonstrating the peak corresponding to the (111) plane.
In other research, (Li, et al ., 2013) synthesized nanostructures of a copper telluride of varying shapes, such as rods, plates, and cubes, and their XRD experiment discovered that the relative intensities were correlated with the nanoparticles’ shapes.
Another group, (Upadhyaya, Parekh, & Pandey, 2016) applied the X-ray line broadening technique and determined the magnetite nanoparticles’ average crystallite size, which they discovered was in the 9–53 nm range. Their findings implied the crystallite’s lattice strain and size impacted the XRD peak broadening. The team also found that the technique is not appropriate for differentiating the boundaries between the two crystallite lattice, and the real transmission electron microscopy (TEM) size of a few samples calculated from the Scherrer formula were bigger than 50-55 nm.
Future Developments
Nanoparticles are usually produced in low quantity on the lab scale, making them challenging for sample preparation and screening.
In the future, improvement in the accuracy and resolution of XRD should be of primary focus. The synthesis of nanoparticles that have diverse physio-chemical, electronic, mechanical, and optical properties have huge demand and they require credible and precise protocols for characterization. In practice, the current characterizations tools for nanoparticles bear some unavoidable errors and compared to that of bulk materials, are difficult to analyze. A comprehensive approach to characterization is appreciated and the best results may yield if XRD is complemented with other instrumental methods.
References and Further Reading
Fultz, B., & Howe, J. (2013). Transmission Electron Microscopy and Diffractometry of Materials. Springer. doi:10.1007/978-3-642-29761-8
Koczkur, K., Mourdikoudis, S., Polavarapu, L., & Skrabalak, S. (2015). Polyvinylpyrrolidone (PVP) in nanoparticle synthesis. Dalton Transactions . doi:10.1039/C5DT02964C
Li, W., Zamani, R., Gil, P., Pelaz, B., Ibáñez, M., Cadavid, D., . . . Alvarez-Puebla, R. (2013). CuTe nanocrystals: shape and size control, plasmonic properties, and use as SERS probes and photothermal agents. J Am Chem Soc . doi:10.1021/ja401428e
Mourdikoudis, S., Pallares, R., & Thanh, N. (2018). Characterization techniques for nanoparticles: comparison and complementarity upon studying nanoparticle properties. Nanoscale . doi:10.1039/C8NR02278J
Thanh, N., Maclean, N., & Mahiddine, S. (2014). Mechanisms of Nucleation and Growth of Nanoparticles in Solution. Chem. Rev. doi:10.1021/cr400544s
Upadhyaya, S., Parekh, K., & Pandey, B. (2016). Influence of crystallite size on the magnetic properties of Fe3O4 nanoparticles. Journal of Alloys and Compounds . doi:10.1016/j.jallcom.2016.03.279
Widjonarko, N. (2016). Introduction to Advanced X-ray Diffraction Techniques for Polymeric Thin Films. Coatings . doi:10.3390/coatings6040054
Wu, S., Yan, S., Qi, W., Huang, R., Cui, J., Su, R., & He, Z. (2015). Green synthesis of gold nanoparticles using aspartame and their catalytic activity for p-nitrophenol reduction. Nanoscale Research Letters . doi:10.1186/s11671-015-0910-7
Disclaimer: The views expressed here are those of the author expressed in their private capacity and do not necessarily represent the views of AZoM.com Limited T/A AZoNetwork the owner and operator of this website. This disclaimer forms part of the Terms and conditions of use of this website.

Dr. Parva Chhantyal
After graduating from The University of Manchester with a Master's degree in Chemical Engineering with Energy and Environment in 2013, Parva carried out a PhD in Nanotechnology at the Leibniz University Hannover in Germany. Her work experience and PhD specialized in understanding the optical properties of Nano-materials. Since completing her PhD in 2017, she is working at Steinbeis R-Tech as a Project Manager.
Please use one of the following formats to cite this article in your essay, paper or report:
Chhantyal, Parva. (2022, March 22). The Use of X-Ray Diffraction for Nanoparticle Characterization. AZoOptics. Retrieved on July 09, 2024 from https://www.azooptics.com/Article.aspx?ArticleID=2180.
Chhantyal, Parva. "The Use of X-Ray Diffraction for Nanoparticle Characterization". AZoOptics . 09 July 2024. <https://www.azooptics.com/Article.aspx?ArticleID=2180>.
Chhantyal, Parva. "The Use of X-Ray Diffraction for Nanoparticle Characterization". AZoOptics. https://www.azooptics.com/Article.aspx?ArticleID=2180. (accessed July 09, 2024).
Chhantyal, Parva. 2022. The Use of X-Ray Diffraction for Nanoparticle Characterization . AZoOptics, viewed 09 July 2024, https://www.azooptics.com/Article.aspx?ArticleID=2180.

Useful information 👌👏
The opinions expressed here are the views of the writer and do not necessarily reflect the views and opinions of AZoOptics.com.
Tell Us What You Think
Do you have a review, update or anything you would like to add to this article?
Cancel reply to comment
- Trending News Stories
Featured Equipment
Latest interviews, trending stories.

Quasicrystal Metasurfaces: Dual-Function Holography and Diffraction Technology

Optical Module Enhances Satellite Lens Versatility

All-Optical Imager Captures Phase and Amplitude Simultaneously

New Thin-Film Membranes Revolutionize Infrared Imaging

New Technique Uses Sound Waves to Steer Objects Underwater

Advanced F-Theta Lenses for Precision Imaging Systems
These F-theta lenses by Avantier are designed for consistent spot size and uniform field curvature correction, ideal for high-resolution imaging applications.

Off-Axis Parabolic (OAP) Mirrors: Precision Solutions for Advanced Optical Systems
Shanghai Optics provides high-precision off-axis parabolic (OAP) mirrors designed for advanced optical systems, offering superior reflective solutions for applications requiring precise light collimation and focus.

MIRcat Mid-IR Laser: Superior High-Speed, Broad-Spectrum Capabilities
The MIRcat Mid-IR Laser provides high-speed, broad-spectrum capabilities with peak tuning velocities up to 30,000 cm1/s.
Advancing Laser Technology: Ophir Discusses the Importance of Measuring M2
Reuven Silverman
Reuven Silverman of Ophir discusses the critical role of M2 measurements in laser technology for optimization and quality control in various industries.

Nuclear Inspection – The Challenges for Optical Systems Now and in the Future
Rob Watkinson
In this interview, AZoOptics speaks to Rob Watkinson about the challenges for optical systems in nuclear inspection.

New X-Ray Technique Allows Effective Imaging of Living Organisms
Rebecca Spiecker
AZoOptics features a new interview with Rebecca Spiecker of the Karlsruhe Institute of Technology, discussing the development of a new X-ray technique that allows better imaging and analysis of living organisms.

Most Read Articles

DNA Origami: Illuminating the Future of Photonics

Ultrasonic Techniques for Lithium-Ion Battery Diagnostics

The Role of Mass Spectrometry in Protein Analysis

X-Ray Diffraction vs. X-Ray Fluorescence

What is Photoemission Spectroscopy?

Understanding Spherical Mirrors: A Comprehensive Guide to Concepts and Applications
Sponsored content, enhancing ophthalmic exams: the role of two-aspheric lenses in optical advancements, ruggedised custom lenses for industrial & outdoor applications, what are optical filters types and applications, beyond optical stereo microscopy, newsletters you may be interested in.
Your AI Powered Scientific Assistant
Hi, I'm Azthena, you can trust me to find commercial scientific answers from AZoNetwork.com.
A few things you need to know before we start. Please read and accept to continue.
- Use of “Azthena” is subject to the terms and conditions of use as set out by OpenAI .
- Content provided on any AZoNetwork sites are subject to the site Terms & Conditions and Privacy Policy .
- Large Language Models can make mistakes. Consider checking important information.
Great. Ask your question.
Azthena may occasionally provide inaccurate responses. Read the full terms .
While we only use edited and approved content for Azthena answers, it may on occasions provide incorrect responses. Please confirm any data provided with the related suppliers or authors. We do not provide medical advice, if you search for medical information you must always consult a medical professional before acting on any information provided.
Your questions, but not your email details will be shared with OpenAI and retained for 30 days in accordance with their privacy principles.
Please do not ask questions that use sensitive or confidential information.
Read the full Terms & Conditions .
Provide Feedback
Current applications of x-ray powder diffraction - A review
- October 2014
- 38(2):95-109

- Stony Brook University

- University of Malaya

Discover the world's research
- 25+ million members
- 160+ million publication pages
- 2.3+ billion citations
- Arpita Gope

- Priyajit CHATTERJEE

- Tengjiao Liu
- Jianqi Wang
- Kavvyasruthi Uj

- Priya Patel

- Krishna Butani

- Carlos A. Nogueira
- Charles Kittel

- H.G. Brittain

- Eiichiro Matsubara
- Kozo Shinoda
- A. P. Voskamp
- Ragnar Österlund
- P. C. Becker

- Chuan-Bi Li
- PROG POLYM SCI

- Recruit researchers
- Join for free
- Login Email Tip: Most researchers use their institutional email address as their ResearchGate login Password Forgot password? Keep me logged in Log in or Continue with Google Welcome back! Please log in. Email · Hint Tip: Most researchers use their institutional email address as their ResearchGate login Password Forgot password? Keep me logged in Log in or Continue with Google No account? Sign up
RSC Advances
The determination of 11 sulfonamide antibiotics in water and foods by developing a n-rich magnetic covalent organic framework combined with ultra-high performance liquid chromatography-tandem mass spectrometry †.

* Corresponding authors
a Shijiazhuang Center for Disease Control and Prevention, Shijiazhuang 050011, China E-mail: [email protected] , [email protected]
b Shijiazhuang Technology Innovation Center for Chemical Poison Detection and Risk Early Warning, Shijiazhuang 050011, China
c Weifang Customs, Weifang 261041, China E-mail: [email protected]
The concentration of antibiotic residues in water and animal-derived foods is low and the matrix is complex, and effective extraction of antibiotic residues in them is a key factor for accurate quantification. It is important to establish a rapid and effective method for the analytical determination of antibiotics in water and foods. In this study, a type of novel magnetic COF (Fe 3 O 4 @SiO 2 @PDE-TAPB-COF) was synthesized and characterized. Moreover, Fe 3 O 4 @SiO 2 @PDE-TAPB-COF combined with ultra-high performance liquid chromatography-tandem mass spectrometry was used to determine the 11 sulfonamide antibiotics (SAs) in water and food. The parameters including pH, adsorption amount, adsorption time, type of elution solvent and elution time were optimized. Under the optimal conditions, the standard curves of 11 SAs showed good linearity ( R 2 > 0.999) in their respective concentration ranges and had lower detection and quantification limits. The spiked recoveries of the developed MSPE-UPLC-MS/MS method for the 11 SAs in water and foods were 74.3–107.2% and 75.1–102.5%, respectively. And the relative standard deviations (RSDs) were less than 9.56% ( n = 7). The results indicated that the method can be used for the determination of SAs in foods and water with low detection limits and high sensitivity.

Supplementary files
- Supplementary information PDF (195K)
Article information
Download Citation
Permissions.
The determination of 11 sulfonamide antibiotics in water and foods by developing a N-rich magnetic covalent organic framework combined with ultra-high performance liquid chromatography-tandem mass spectrometry
L. Ma, Y. Gu, L. Guo and K. Wang, RSC Adv. , 2024, 14 , 21318 DOI: 10.1039/D4RA02530J
This article is licensed under a Creative Commons Attribution-NonCommercial 3.0 Unported Licence . You can use material from this article in other publications, without requesting further permission from the RSC, provided that the correct acknowledgement is given and it is not used for commercial purposes.
To request permission to reproduce material from this article in a commercial publication , please go to the Copyright Clearance Center request page .
If you are an author contributing to an RSC publication, you do not need to request permission provided correct acknowledgement is given.
If you are the author of this article, you do not need to request permission to reproduce figures and diagrams provided correct acknowledgement is given. If you want to reproduce the whole article in a third-party commercial publication (excluding your thesis/dissertation for which permission is not required) please go to the Copyright Clearance Center request page .
Read more about how to correctly acknowledge RSC content .
Social activity
Search articles by author, advertisements.
Crystallographic analysis of graphite by X-Ray diffraction
- Published: 04 January 2018
- Volume 60 , pages 361–365, ( 2017 )
Cite this article

- A. N. Popova 1
3125 Accesses
Explore all metrics
X-ray diffraction is a widely used nondestructive method of studying carbon materials. It is employed to study the phase composition of samples, to analyze the qualitative and quantitative composition of specific phases, and to assess the structural characteristics of crystalline carbon materials. In the present work, we calculate the basic structural parameters of graphite after various treatments. The crystalline structure of structure is most commonly characterized by the interplane distance d 00 l , the dimensions of the structural components L a and L c , and the degree of order. The nonuniformity of the phase compositions is described by comparing data from the primary crystallographic reflexes of the (00 l ) series, corresponding to the basic plane of graphite. The (002), (004), and (006) reflexes represent the superposition of components characterizing individual structural phases of the samples, with specific interplane distances. By resolution of the reflexes into structural components, an additional characteristic of the sample may be derived: the ratio of the phases. On that basis, the crystalline structure of samples with similar overall structural characteristics may be more accurately characterized.
This is a preview of subscription content, log in via an institution to check access.
Access this article
Subscribe and save.
- Get 10 units per month
- Download Article/Chapter or Ebook
- 1 Unit = 1 Article or 1 Chapter
- Cancel anytime
Price includes VAT (Russian Federation)
Instant access to the full article PDF.
Rent this article via DeepDyve
Institutional subscriptions
Similar content being viewed by others

X-ray diffraction analysis of the crystal structures of different graphites
Possibilities of powder x-ray diffraction methods in determining structural characteristics of carbon materials, analyzing products of the electrochemical exfoliation of graphite via rutherford backscattering spectrometry and x-ray diffractometry.
Buraya, I.D., Vovochenko, L.L., Voznaya, L.L., et al., Influence of conditions of thermochemical treatment of natural graphite on its crystal structure and electrophysical properties, Khim. Tverd. Tela , 1990, no. 6, pp. 104–108.
CAS Google Scholar
Dyadin, Yu.A., Graphite and its inclusions, Sorosovskii Obraz. Zh. , 2000, vol. 6, no. 10, pp. 43–49.
Google Scholar
Titel’man, G.I., Pechkin, S.V., Gel’man, V.N., et al., Thermal splitting of graphite-acid decomposition products under the shock and linear heating, Khim. Tverd. Tela , 1991, no. 4, pp. 79–84.
Umanskaya, O.I., Abadzheva, R.N., Ishchuk, Yu.L., Fast, A.A., and Mar’yasin, I.L., Influence of physicochemical characteristics of expanded graphite on properties of lubricating greases, Chem. Technol. Fuels Oils , 1988, vol. 24, no. 2, pp. 81–83.
Article Google Scholar
Khokhlova, G.P., Malysheva V.Yu., Barnakov, Ch.N., et al., Influence of the nature and amount of the catalyst on the phase structure of the carbon material obtained by low-temperature catalytic graphitization of coal tar pitch, Vestn. Kuzbass. Gos. Tekh. Univ. , 2013, no. 5, pp. 21–24.
Khokhlova, G.P., Barnakov, Ch.N., Malysheva, V.Yu., Popova, A.N., and Ismagilov, Z.R., Effect of heat treatment conditions on the catalytic graphitization of coal-tar pitch, Solid Fuel Chem. , 2015, vol. 49, no. 2, pp. 66–72.
Article CAS Google Scholar
Khokhlova, G.P., Barnakov, C.N., Popova, A.N., and Khitsova, L.M., Influence of carbon additives on the thermal transformation of coal pitch, Coke Chem. , 2015, vol. 58, no. 7, pp. 268–274.
Khokhlova, G.P., Barnakov, C.N., and Popova, A.N., Carbonization of coal pitch with graphite additives, Coke Chem. , 2016, vol. 59, no. 1, pp. 27–34.
Barnakov, Ch.N., Khokhlova, G.P., Popova, A.N., et al., XRD characterization of the structure of graphites and carbon materials obtained by the low-temperature graphitization of coal tar pitch, Eurasian Chem.- Technol. J. , 2015. V. 17, no. 2. P. 87–93.
Kratkaya khimicheskaya entsiklopediya (Brief Chemical Encyclopedia), Moscow: Sovetskaya Entsiklopediya, 1967, vol. vn5, pp. 303–313.
Fialkov, A.S., Uglegrafitovye materialy (Carbon- Graphite Materials), Moscow: Energiya, 1979.
Trucano, P. and Chen, R., Structure of graphite by neutron-diffraction, Nature , 1975, vol. 258, pp. 136–137.
ICDD, PDF-2 2011 (Database), Kalakkodu, S., Ed., Newtown Square: Int. Centre Diffraction Data, 2011.
Liopo, V.A. and Voina, V.V., Rentgenovskaya difraktometriya: uchebnoe posobie (X-Ray Diffractometry: Manual), Grodno: Grodn. Gos. Univ., 2003.
Download references
Author information
Authors and affiliations.
Federal Research Center of Coal and Coal Chemistry, Siberian Branch, Russian Academy of Sciences, Kemerovo, 650000, Russia
A. N. Popova
You can also search for this author in PubMed Google Scholar
Corresponding author
Correspondence to A. N. Popova .
Additional information
Original Russian Text © A.N. Popova, 2017, published in Koks i Khimiya, 2017, No. 9, pp. 32–36.
About this article
Popova, A.N. Crystallographic analysis of graphite by X-Ray diffraction. Coke Chem. 60 , 361–365 (2017). https://doi.org/10.3103/S1068364X17090058
Download citation
Received : 09 August 2017
Published : 04 January 2018
Issue Date : September 2017
DOI : https://doi.org/10.3103/S1068364X17090058
Share this article
Anyone you share the following link with will be able to read this content:
Sorry, a shareable link is not currently available for this article.
Provided by the Springer Nature SharedIt content-sharing initiative
- X-ray structural analysis
- crystalline structure
- Find a journal
- Publish with us
- Track your research

IMAGES
VIDEO
COMMENTS
X-ray diffraction is a high-tech, nondestructive technique. for analyzing a wide range of materials including fluids, met-. als, minerals, polymers, catalysts, plastics, pharmaceuticals, thin ...
184017. Powder X-ray diffraction (XRD) is a common characterization technique for nanoscale materials. Analysis of a sample by powder XRD provides important information that is complementary to various microscopic and spectroscopic methods, such as phase identification, sample purity, crystallite size, and, in some cases, morphology.
X-ray diffraction analysis typically affords the static 3D structures of given compounds or materials, but to understand chemical processes, the visualization of fast structural changes is desirable.
Experimental Characterization Techniques. Jörgen Bergström, in Mechanics of Solid Polymers, 2015. 2.5.3 X-Ray Diffraction. X-ray diffraction is an important tool for studying both amorphous and semi-crystalline polymers [36, 37].It can be used to analyze many features of the microstructure of the material, including lattice parameters, presence of imperfections, crystallographic orientations ...
X-Ray Diffraction Techniques for Mineral Characterization: A Review for Engineers of the Fundamentals, Applications, and Research Directions December 2021 DOI: 10.20944/preprints202112.0438.v1
The models trained on XRD patterns and virtual PDFs are evaluated using four datasets spanning two chemistries, Li-La-Zr-O and Li-Ti-P-O. To examine how the number of phases in a sample affects ...
Abstract. X-ray diffraction (XRD) is a powerful nondestructive technique for characterizing crystalline materials. It provides information on structures, phases, preferred crystal orientations (texture), and other structural parameters, such as average grain size, crystallinity, strain, and crystal defects.
X-ray diffraction (XRD) is an important and widely used material characterization technique. With the recent development in material science technology and understanding, various new materials are being developed, which requires upgrading the existing analytical techniques such that emerging intricate problems can be solved. Although XRD is a well-established non-destructive technique, it ...
Powder x-ray diffraction (XRD) is the golden standard for material characterization, where it produces a pattern that encodes information about the crystal symmetry, lattice parameters, types, and ...
The Canadian Journal of Chemical Engineering publishes influential research about the science, theory, and industrial practices of chemical and biochemical processes. Abstract X-ray diffraction (XRD) analysis identifies the long-range order (ie, the structure) of crystalline materials and the short-range order of non-crystalline materials.
Powder XRD is a compact advanced instrument (Figure 1). It has. various salient features and new accessories like variable temperature. assembly and humidity chamber that can further expand the ...
X-ray diffraction (XRD) techniques are powerful, non-destructive characterization tool with minimal sample preparation. XRD provides the first information about the materials phases, crystalline structure, average crystallite size, micro and macro strain, orientation parameter, texture coefficient, degree of crystallinity, crystal defects etc. XRD analysis provides information about the bulk ...
View a PDF of the paper titled DeepXRD, a Deep Learning Model for Predicting of XRD spectrum from Materials Composition, by Rongzhi Dong and 8 other authors View PDF Abstract: One of the long-standing problems in materials science is how to predict a material's structure and then its properties given only its composition.
Although various researched works have been carried out in x-ray crystallography and its applications, but there are still limited number of researches on crystallographic theories and industrial application of x-ray diffraction. The present study reviewed and provided detailed discussion on atomic arrangement of single crystals, mathematical concept of Bravais, reciprocal lattice, and ...
Powder X-Ray diffraction (XRD) patterns are the most fundamental and frequently encountered type of structural data in inorganic materials science. [1-9] We suggest that the powder XRD pattern should be used as a material descriptor for the symmetry identification and property prediction based on machine learning (ML) (or deep learning [DL ...
X-ray diffraction (XRD) is a powerful nondestructive technique for characterizing crystalline materials. It provides information on structures, phases, preferred crystal orientations (texture), and other structural parameters, such as average grain size, crystallinity, strain, and crystal defects. X-ray diffraction peaks are produced by ...
X-ray diffraction (XRD) data acquisition and analysis is among the most time-consuming steps in the development cycle of novel thin-film materials. We propose a machine learning-enabled approach ...
By Dr. Parva Chhantyal, Ph.D. Mar 21 2022. X-ray diffraction (XRD) is a versatile technique used commonly in the field of nanotechnology to characterize and acquire accurate information regarding ...
The single-crystal XRD study confirms the structure of 1 as [H 3 O] 4 [Cu 7 (NH 3) 2 (H 2 O) 4 {B 24 O 39 (OH) 12}]·13H 2 O. The structure is comprised of an anionic cluster, [Cu 7 (NH 3) 2 (H 2 O) 4 {B 24 O 39 (OH) 12}] 4− with idealized C 2v symmetry and seventeen (disordered) molecules of H 2 O. Four of the seventeen H 2 O molecules are required to be protonated in order to balance the ...
X-ray diffraction (XRD) data analysis can be a time-consuming and laborious task. Deep neural network (DNN) based models trained with synthetic XRD patterns have been proven to be a highly efficient, accurate, and automated method for analyzing common XRD data collected from solid samples in ambient environments. However, it remains unclear whether synthetic XRD-based models can be effective ...
The X-ray diffraction (XRD) analysis was carried out in order to investigate the phase composition and crystalline behavior of the as-synthesized n-HA. This analysis was performed in a Rigaku, MiniFlex II X-ray diffractometer equipped with a CuKα radiation ( λ =0.15406 nm), acceleration voltage of 30 kV, and a current of 15 mA.
Figure 5 a showed the XRD pattern observed from the synthesized nanoparticles of fresh leaves of P. acidus. The four distinct diffraction peaks at 2ɵ values of 38.05°, 44.23°, 64.41°, and 76. ...
Paper. Submitted 03 Apr 2024. Accepted 21 Jun 2024. First published 08 Jul 2024. This article is Open Access. Download Citation. RSC Adv., 2024, 14, 21318-21327 Permissions. Request permissions The determination of 11 sulfonamide antibiotics in water and foods by developing a N-rich magnetic covalent organic framework combined with ultra-high ...
X-ray diffraction is a widely used nondestructive method of studying carbon materials. It is employed to study the phase composition of samples, to analyze the qualitative and quantitative composition of specific phases, and to assess the structural characteristics of crystalline carbon materials. In the present work, we calculate the basic structural parameters of graphite after various ...